不等式選講.
設函數(shù)
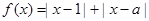
.
(1)若
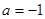
解不等式
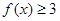
;
(2)如果關于
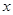
的不等式
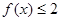
有解,求
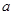
的取值范圍.
試題分析:(Ⅰ)當
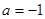
時,

由
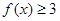
,得,
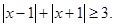
①當
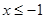
時,不等式化為

即

所以,原不等式的解為

②當
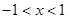
時,不等式化為
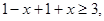
即

所以,原不等式無解.
③ 當

時,不等式化為

即

所以,原不等式的解為

綜上,原不等式的解為

5分
(說明:若考生按其它解法解答正確,相應給分)
(Ⅱ)因為關于
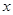
的不等式
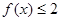
有解,所以,

因為

表示數(shù)軸上的點到

與
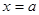
兩點的距離之和,
所以,
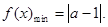

解得,
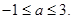
所以,
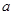
的取值范圍為

10分
點評:中檔題,絕對值不等式的解法,往往從“去”絕對值的符號入手,主要方法有“平方法”“分類討論法”,有時利用絕對值的幾何意義,會簡化解題過程。
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
設函數(shù)f(x)=|2x+1|-|x-2|.
(Ⅰ)求不等式
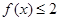
的解集;
(Ⅱ)若{x|f(x)≥
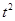
-t}∩{y|0≤y≤1}≠
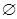
,求實數(shù)t的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)

(I)當

時,求不等式

的解集;
(Ⅱ)若

的解集包含

,求

的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
不等式

的解集為_________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設函數(shù)
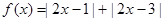
,
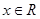
.
(1)解不等式:
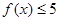
;
(2)若
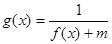
的定義域為
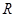
,求實數(shù)
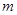
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)

(1)當
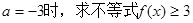
的解集
(2)若
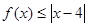
的解集包含[1,2],求
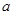
的取值范圍
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
若不等式
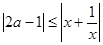
對一切非零實數(shù)
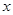
恒成立,則實數(shù)
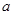
的取值范圍是
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
不等式

的解集為__
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設
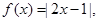
若不等式
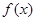
≥
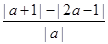
對任意實數(shù)
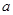
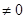
恒成立,則
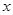
的取值集合是________________.
查看答案和解析>>

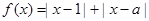 .
.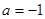 解不等式
解不等式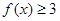 ;
;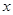 的不等式
的不等式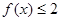 有解,求
有解,求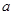 的取值范圍.
的取值范圍.  學業(yè)測評一課一測系列答案
學業(yè)測評一課一測系列答案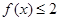 的解集;
的解集;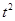 -t}∩{y|0≤y≤1}≠
-t}∩{y|0≤y≤1}≠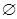 ,求實數(shù)t的取值范圍.
,求實數(shù)t的取值范圍.