
【題目】自新型冠狀病毒疫情爆發以來,人們時刻關注疫情,特別是治愈率,治愈率![]() 累計治愈人數/累計確診人數,治愈率的高低是“戰役”的重要數據,由于確診和治愈人數在不斷變化,那么人們就非常關心第
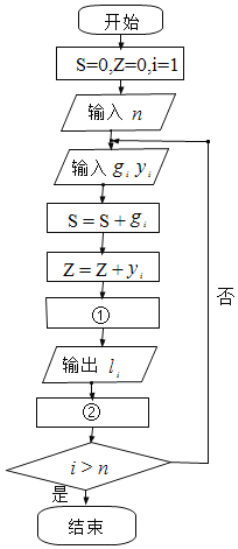
累計治愈人數/累計確診人數,治愈率的高低是“戰役”的重要數據,由于確診和治愈人數在不斷變化,那么人們就非常關心第![]() 天的治愈率,以此與之前的治愈率比較,來推斷在這次“戰役”中是否有了更加有效的手段,下面是一段計算治愈率的程序框圖,請同學們選出正確的選項,分別填入①②兩處,完成程序框圖.( )
天的治愈率,以此與之前的治愈率比較,來推斷在這次“戰役”中是否有了更加有效的手段,下面是一段計算治愈率的程序框圖,請同學們選出正確的選項,分別填入①②兩處,完成程序框圖.( )
![]() :第
:第![]() 天新增確診人數;
天新增確診人數;![]() :第
:第![]() 天新增治愈人數;
天新增治愈人數;![]() :第
:第![]() 天治愈率
天治愈率
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
科目:高中數學 來源: 題型:
【題目】2019年春節期間,某超市準備舉辦一次有獎促銷活動,若顧客一次消費達到400元則可參加一次抽獎活動,超市設計了兩種抽獎方案.
方案一:一個不透明的盒子中裝有30個質地均勻且大小相同的小球,其中10個紅球,20個白球,攪拌均勻后,顧客從中隨機抽取一個球,若抽到紅球則顧客獲得60元的返金券,若抽到白球則獲得20元的返金券,且顧客有放回地抽取3次.
方案二:一個不透明的盒子中裝有30個質地均勻且大小相同的小球,其中10個紅球,20個白球,攪拌均勻后,顧客從中隨機抽取一個球,若抽到紅球則顧客獲得80元的返金券,若抽到白球則未中獎,且顧客有放回地抽取3次.
(1)現有兩位顧客均獲得抽獎機會,且都按方案一抽獎,試求這兩位顧客均獲得180元返金券的概率;
(2)若某顧客獲得抽獎機會.
①試分別計算他選擇兩種抽獎方案最終獲得返金券的數學期望;
②為了吸引顧客消費,讓顧客獲得更多金額的返金券,該超市應選擇哪一種抽獎方案進行促銷活動?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖統計了截止到2019年年底中國電動汽車充電樁細分產品占比及保有量情況,關于這5次統計,下列說法正確的是( )
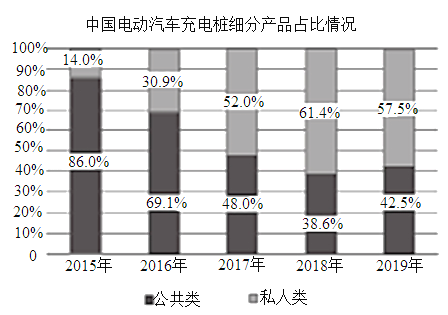
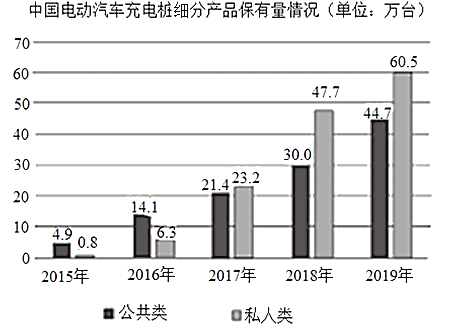
A.私人類電動汽車充電樁保有量增長率最高的年份是2018年
B.公共類電動汽車充電樁保有量的中位數是25.7萬臺
C.公共類電動汽車充電樁保有量的平均數為23.12萬臺
D.從2017年開始,我國私人類電動汽車充電樁占比均超過50%
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,
,![]() 、
、![]() 為橢圓的左、右焦點,
為橢圓的左、右焦點,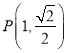 為橢圓上一點,且
為橢圓上一點,且![]() .
.
(1)求橢圓的標準方程;
(2)設直線![]() ,過點
,過點![]() 的直線交橢圓于
的直線交橢圓于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的垂直平分線分別交直線
的垂直平分線分別交直線![]() 、直線
、直線![]() 于
于![]() 、
、![]() 兩點,當
兩點,當![]() 最小時,求直線
最小時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線C:![]() 與直線
與直線![]() 交于A、B兩點.
交于A、B兩點.
(1)當![]() 取得最小值為
取得最小值為![]() 時,求
時,求![]() 的值.
的值.
(2)在(1)的條件下,過點![]() 作兩條直線PM、PN分別交拋物線C于M、N(M、N不同于點P)兩點,且
作兩條直線PM、PN分別交拋物線C于M、N(M、N不同于點P)兩點,且![]() 的平分線與
的平分線與![]() 軸平行,求證:直線MN的斜率為定值.
軸平行,求證:直線MN的斜率為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某地區某高傳染性病毒流行期間,為了建立指標顯示疫情已受控制,以便向該地區居民顯示可以過正常生活,有公共衛生專家建議的指標是“連續7天每天新增感染人數不超過5人”,根據連續7天的新增病例數計算,下列各個選項中,一定符合上述指標的是__________.
①平均數![]() ; ②標準差
; ②標準差![]() ; ③平均數
; ③平均數![]() 且標準差
且標準差![]() ;
;
④平均數![]() 且極差小于或等于2; ⑤眾數等于1且極差小于或等于4.
且極差小于或等于2; ⑤眾數等于1且極差小于或等于4.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,右頂點為
,右頂點為![]() ,右焦點為
,右焦點為![]() ,
,![]() 為坐標原點,
為坐標原點,![]() ,橢圓
,橢圓![]() 過點
過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() (
(![]() 在
在![]() 之間),求
之間),求![]() 與
與![]() 面積之比的取值范圍.
面積之比的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com