
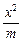 +
+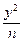 =1(m>n>0)和雙曲線
=1(m>n>0)和雙曲線 -
-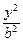 =1(a>b>0)有相同的焦點F1、F2,P是兩條曲線的一個交點,則|PF1|·|PF2|的值是
=1(a>b>0)有相同的焦點F1、F2,P是兩條曲線的一個交點,則|PF1|·|PF2|的值是| A.m-a | B.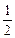 (m-a) (m-a) |
| C.m2-a2 | D.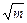 - -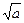 |
 孟建平錯題本系列答案
孟建平錯題本系列答案 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
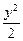 =1,過點A(2,1)的直線l與已知雙曲線交于P1、P2兩點.
=1,過點A(2,1)的直線l與已知雙曲線交于P1、P2兩點.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
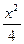 -y2=1.
-y2=1.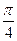 ,被雙曲線截得的弦長為
,被雙曲線截得的弦長為
 ,求直線l的方程;
,求直線l的方程;查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
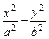 =1的右焦點是F,右頂點是A,虛軸的上端點是B,
=1的右焦點是F,右頂點是A,虛軸的上端點是B,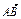 ·
·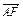 =6-4
=6-4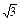 ,∠BAF=150°.
,∠BAF=150°.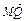 +2
+2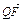 =0,求直線l的斜率.
=0,求直線l的斜率.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
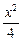 -
-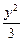 =-1有兩個交點,則直線l的斜率的取值范圍是
=-1有兩個交點,則直線l的斜率的取值范圍是A.(-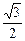 , ,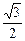 ) ) |
B.(-∞,-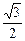 )∪( )∪(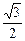 ,+∞) ,+∞) |
C.[-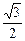 , ,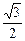 ] ] |
D.(-∞,-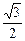 ]∪[ ]∪[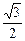 ,+∞) ,+∞) |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
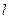 有兩個不同的交點,求證:
有兩個不同的交點,求證: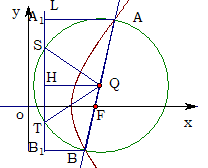
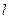 截得圓弧的度數(shù)為定值.
截得圓弧的度數(shù)為定值.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題


 的離心率為
的離心率為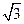 ,右準線方程為
,右準線方程為 。
。 與雙曲線C交于不同的兩點A,B,且線段AB的中點在圓
與雙曲線C交于不同的兩點A,B,且線段AB的中點在圓 上,求m的值.
上,求m的值. 查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com