
【題目】已知曲線C1: ![]() ,(t為參數)曲線C2:
,(t為參數)曲線C2: ![]() +y2=4.
+y2=4.
(1)在同一平面直角坐標系中,將曲線C2上的點按坐標變換y′=yx,后得到曲線C′.求曲線C′的普通方程,并寫出它的參數方程;
(2)若C1上的點P對應的參數為t= ![]() ,Q為C′上的動點,求PQ中點M到直線C3:
,Q為C′上的動點,求PQ中點M到直線C3: ![]() (t為參數)的距離的最小值.
(t為參數)的距離的最小值.
【答案】
(1)解:由 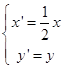 得到
得到 ![]() ①
①
將①代入曲線C2: ![]() +y2=4.得
+y2=4.得 ![]() +(y′)2=4,即(x′)2+(y′)2=4.
+(y′)2=4,即(x′)2+(y′)2=4.
因此橢圓 ![]() +y2=4經伸縮變換后得到的曲線方程是x2+y2=4.
+y2=4經伸縮變換后得到的曲線方程是x2+y2=4.
它的參數方程為 ![]()
(2)解:當t=π/2時,P(﹣4,4),Q(2cosθ,2sinθ),故M(﹣2+cosθ,2+sinθ)
曲線C3:為直線x﹣2y+8=0,
M到C3的距離d= ![]() |(﹣2+cosθ)﹣2(2+sinθ)+8|=
|(﹣2+cosθ)﹣2(2+sinθ)+8|= ![]() |cosθ﹣2sinθ+2|=
|cosθ﹣2sinθ+2|= ![]() |
| ![]() cos(θ+α)+2|
cos(θ+α)+2|
從而tanα=2時d的最小值為 ![]() |﹣
|﹣ ![]() +2|=
+2|= ![]()
【解析】(1)由 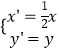 得到
得到 ![]() ,代入曲線C2:
,代入曲線C2: ![]() +y2=4.化簡可得橢圓
+y2=4.化簡可得橢圓 ![]() +y2=4經伸縮變換后得到的曲線方程.利用平方關系可得它的參數方程.(2)當t=
+y2=4經伸縮變換后得到的曲線方程.利用平方關系可得它的參數方程.(2)當t= ![]() 時,P(﹣4,4),Q(2cosθ,2sinθ),故M(﹣2+cosθ,2+sinθ).曲線C3:為直線x﹣2y+8=0,利用點到直線的距離公式可得M到C3的距離d=
時,P(﹣4,4),Q(2cosθ,2sinθ),故M(﹣2+cosθ,2+sinθ).曲線C3:為直線x﹣2y+8=0,利用點到直線的距離公式可得M到C3的距離d= ![]() |
| ![]() cos(θ+α)+2|,利用三角函數的單調性即可得出.
cos(θ+α)+2|,利用三角函數的單調性即可得出.


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】古希臘杰出的數學家丟番圖的墓碑上有這樣一首詩:
這是一座古墓,里面安葬著丟番圖.
請你告訴我,丟番圖的壽數幾何?
他的童年占去了一生的六分之一,
接著十二分之一是少年時期,
又過了七分之一的時光,他找到了自己的終身伴侶.
五年之后,婚姻之神賜給他一個兒子,
可是兒子不濟,只活到父親壽數的一半,就匆匆離去.
這對父親是一個沉重的打擊,
整整四年,為失去愛子而悲傷,
終于告別了數學,離開了人世.
試用循環結構,寫出算法分析和算法程序.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋子中放有大小和形狀相同的小球若干個,其中標號為0的小球1個,標號為1的小球1個,標號為2的小球n個.已知從袋子中隨機抽取1個小球,取到標號是2的小球的概率是![]() .
.
(1)求n的值;
(2)從袋子中不放回地隨機抽取2個小球,記第一次取出的小球標號為a,第二次取出的小球標號為b.
①記事件A表示“a+b=2”,求事件A的概率;
②在區間[0,2]內任取2個實數x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() ,周期是
,周期是![]() .
.
(1)求函數解析式,并寫出函數圖象的對稱軸方程和對稱中心;
(2)已知點![]() ,點
,點![]() 是該函數圖象上一點,點
是該函數圖象上一點,點![]() 是
是![]() 的中點,當
的中點,當![]() ,
, ![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電子商務公司對10 000名網絡購物者2017年度的消費情況進行統計,發現消費金額(單位:萬元)都在區間[0.3,0.9]內,其頻率分布直方圖如圖所示.
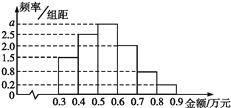
(1)直方圖中的a=_____;
(2)在這些購物者中,消費金額在區間[0.5,0.9]內的購物者的人數為_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設X是一個離散型隨機變量,則下列不能成為X的概率分布列的一組數據是( )
A.0, ![]() ,0,0,
,0,0, ![]()
B.0.1,0.2,0.3,0.4
C.p,1﹣p(0≤p≤1)
D.![]() ,
, ![]() ,…,
,…, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知全集U=R,集合A={x|1<2x<8},B={x| ![]() +1<0},C={x|a<x<a+1}.
+1<0},C={x|a<x<a+1}.
(1)求集合UA∩B;
(2)若B∪C=B,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com