
【題目】已知直線l:![]() ,半徑為4的圓C與直線l相切,圓心C在x軸上且在直線l的右上方.
,半徑為4的圓C與直線l相切,圓心C在x軸上且在直線l的右上方.
(Ⅰ)求圓C的方程;
(Ⅱ)過點M (2,0)的直線與圓C交于A,B兩點(A在x軸上方),問在x軸正半軸上是否存在定點N,使得x軸平分∠ANB?若存在,請求出點N的坐標;若不存在,請說明理由.
【答案】(Ⅰ)x2+y2=16.(Ⅱ)存在點N為(8,0)時,能使得∠ANM=∠BNM總成立.
【解析】分析:(Ⅰ)根據已知求得a=0,可以求出圓C的方程. (Ⅱ)分AB有斜率和沒有斜率兩種情況討論,當AB有斜率時,x軸平分∠ANB, 則kAN=-kBN ,即可求出t的值.
詳解:(Ⅰ)設圓心C(a,0) (![]() ),
),
則![]() a=0或a=
a=0或a=![]() (舍).
(舍).
所以圓C的方程為x2+y2=16.
(Ⅱ)當直線AB⊥x軸時,x軸平分∠ANB.
當直線AB的斜率存在時,設直線AB的方程為y=k(x-2),
假設N(t,0) ![]() 符合題意,又設A(x1,y1),B(x2,y2),
符合題意,又設A(x1,y1),B(x2,y2),
由![]() 得(k2+1)x2-4k2x+4k2-16=0,
得(k2+1)x2-4k2x+4k2-16=0,
所以x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
若x軸平分∠ANB, 則kAN=-kBN
即![]() +
+![]() =0
=0![]() +
+![]() =0
=0
2x1x2-(t+2)(x1+x2)+4t=0
![]() -
-![]() +4t=0t=8.
+4t=0t=8.
所以存在點N為(8,0)時,能使得∠ANM=∠BNM總成立.


科目:高中數學 來源: 題型:
【題目】定義:曲線C上的點到直線l的距離的最小值稱為曲線C到直線l的距離,已知曲線C1:y=x2+a到直線l:y=x的距離等于曲線C2:x2+(y+4)2=2到直線l:y=x的距離,則實數a= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設m,n∈R,若直線(m+1)x+(n+1)y﹣2=0與圓(x﹣1)2+(y﹣1)2=1相切,則m+n的取值范圍是( )
A.[1﹣ ![]() ,1+
,1+ ![]() ]
]
B.(﹣∞,1﹣ ![]() ]∪[1+
]∪[1+ ![]() ,+∞)
,+∞)
C.[2﹣2 ![]() ,2+2
,2+2 ![]() ]
]
D.(﹣∞,2﹣2 ![]() ]∪[2+2
]∪[2+2 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1. 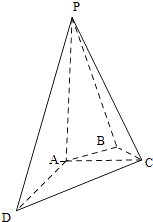
(1)證明:PC⊥AD;
(2)求二面角A﹣PC﹣D的正弦值;
(3)設E為棱PA上的點,滿足異面直線BE與CD所成的角為30°,求AE的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,半徑為R的半球O的底面圓O在平面α內,過點O作平面α的垂線交半球面于點A,過圓O的直徑CD作平面α成45°角的平面與半球面相交,所得交線上到平面α的距離最大的點為B,該交線上的一點P滿足∠BOP=60°,則A、P兩點間的球面距離為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年6月14日,第二十一屆世界杯尼球賽在俄羅斯拉開了帷幕,某大學在二年級作了問卷調查,從該校二年級學生中抽取了![]() 人進行調查,其中女生中對足球運動有興趣的占
人進行調查,其中女生中對足球運動有興趣的占![]() ,而男生有
,而男生有![]() 人表示對足球運動沒有興趣.
人表示對足球運動沒有興趣.
(1)完成![]() 列聯表,并回答能否有
列聯表,并回答能否有![]() 的把握認為“對足球是否有興趣與性別有關”?
的把握認為“對足球是否有興趣與性別有關”?
有興趣 | 沒有興趣 | 合計 | |
男 |
| ||
女 | |||
合計 |
(2)若將頻率視為概率,現再從該校二年級全體學生中,采用隨機抽樣的方法每飲抽取![]() 名學生,抽取
名學生,抽取![]() 次,記被抽取的
次,記被抽取的![]() 名學生中對足球有興趣的人數為
名學生中對足球有興趣的人數為![]() ,若每次抽取的結果是相互獨立的,求
,若每次抽取的結果是相互獨立的,求![]() 的分布列和數學期望.
的分布列和數學期望.
附:
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com