
【題目】若函數![]() 在區間
在區間![]() 上的最大值是
上的最大值是![]() 最小值是
最小值是![]() 則
則![]()
A. 與![]() 有關,且與
有關,且與![]() 有關 B. 與
有關 B. 與![]() 有關,但與
有關,但與![]() 無關
無關
C. 與![]() 無關,且與
無關,且與![]() 無關 D. 與
無關 D. 與![]() 無關,但與
無關,但與![]() 有關
有關
【答案】B
【解析】函數f(x)=x2+ax+b的圖象是開口朝上且以直線x=﹣![]() 為對稱軸的拋物線,
為對稱軸的拋物線,
當﹣![]() >1或﹣
>1或﹣![]() <0,即a<﹣2,或a>0時,
<0,即a<﹣2,或a>0時,
函數f(x)在區間[0,1]上單調,
此時M﹣m=|f(1)﹣f(0)|=|a+1|,
故M﹣m的值與a有關,與b無關
當![]() ≤﹣
≤﹣![]() ≤1,即﹣2≤a≤﹣1時,
≤1,即﹣2≤a≤﹣1時,
函數f(x)在區間[0,﹣![]() ]上遞減,在[﹣
]上遞減,在[﹣![]() ,1]上遞增,
,1]上遞增,
且f(0)>f(1),
此時M﹣m=f(0)﹣f(﹣![]() )=
)=![]() ,
,
故M﹣m的值與a有關,與b無關
當0≤﹣![]() <
<![]() ,即﹣1<a≤0時,
,即﹣1<a≤0時,
函數f(x)在區間[0,﹣![]() ]上遞減,在[﹣
]上遞減,在[﹣![]() ,1]上遞增,
,1]上遞增,
且f(0)<f(1),
此時M﹣m=f(1)﹣f(﹣![]() )=1+a+
)=1+a+![]() ,
,
故M﹣m的值與a有關,與b無關
綜上可得:M﹣m的值與a有關,與b無關
故選B.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,且橢圓
,且橢圓![]() 過點
過點![]() ,離心率
,離心率![]() ;點
;點![]() 在橢圓
在橢圓![]() 上,延長
上,延長![]() 與橢圓
與橢圓![]() 交于點
交于點![]() ,點
,點![]() 是
是![]() 中點.
中點.
(1)求橢圓C的方程;
(2)若![]() 是坐標原點,記
是坐標原點,記![]() 與
與![]() 的面積之和為
的面積之和為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為自然對數的底,
為自然對數的底, ![]() 為常數).
為常數).
(Ⅰ)討論函數![]() 的單調性;
的單調性;
(Ⅱ)對于函數![]() 和
和![]() ,若存在常數
,若存在常數![]() ,對于任意
,對于任意![]() ,不等式
,不等式![]() 都成立,則稱直線
都成立,則稱直線![]() 是函數
是函數![]() 的分界線,設
的分界線,設![]() ,問函數
,問函數![]() 與函數
與函數![]() 是否存在“分界線”?若存在,求出常數
是否存在“分界線”?若存在,求出常數![]() ;若不存在,說明理由.
;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在貫徹中共中央國務院關于精準扶貧政策的過程中,某單位定點幫扶甲、乙兩個村各50戶貧困戶.為了做到精準幫扶,工作組對這100戶村民的年收入情況、勞動能力情況、子女受教育情況、危舊房情況、患病情況等進行調查,并把調查結果轉化為各戶的貧困指標![]() 和
和![]() ,制成下圖,其中“
,制成下圖,其中“![]() ”表示甲村貧困戶,“
”表示甲村貧困戶,“![]() ”表示乙村貧困戶.
”表示乙村貧困戶.
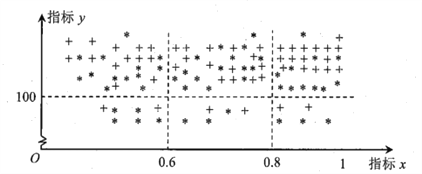
若![]() ,則認定該戶為“絕對貧困戶”,若
,則認定該戶為“絕對貧困戶”,若![]() ,則認定該戶為“相對貧困戶”,若
,則認定該戶為“相對貧困戶”,若![]() ,則認定該戶為“低收入戶”;
,則認定該戶為“低收入戶”;
若![]() ,則認定該戶為“今年能脫貧戶”,否則為“今年不能脫貧戶”.
,則認定該戶為“今年能脫貧戶”,否則為“今年不能脫貧戶”.
(1)從甲村50戶中隨機選出一戶,求該戶為“今年不能脫貧的絕對貧困戶”的概率;
(2)若從所有“今年不能脫貧的非絕對貧困戶”中選3戶,用![]() 表示所選3戶中乙村的戶數,求
表示所選3戶中乙村的戶數,求![]() 的分布列和數學期望
的分布列和數學期望![]() ;
;
(3)試比較這100戶中,甲、乙兩村指標![]() 的方差的大小(只需寫出結論).
的方差的大小(只需寫出結論).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個計算裝置有兩個數據輸入端口I,II與一個運算結果輸出端口III,當I,II分別輸入正整數![]() 時,輸出結果記為
時,輸出結果記為![]() 且計算裝置運算原理如下:
且計算裝置運算原理如下:
①若I,II分別輸入![]() 則
則![]()
②若I輸入固定的正整數![]() II輸入的正整數增大
II輸入的正整數增大![]() 則輸出的結果比原來增大
則輸出的結果比原來增大![]()
③若II輸入![]() I輸入正整數增大
I輸入正整數增大![]() 則輸出結果為原來的
則輸出結果為原來的![]() 倍.則(1)
倍.則(1)![]() =
= ![]() 為正整數);(2)(1)f(m,1)=__,(2)若由f(m,1)得出f(m,n),則滿足f(m,n)=30的平面上的點(m,n)的個數是__.
為正整數);(2)(1)f(m,1)=__,(2)若由f(m,1)得出f(m,n),則滿足f(m,n)=30的平面上的點(m,n)的個數是__.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從高一年級參加期末考試的學生中抽出50名學生,并統計了他們的數學成績(滿分為100分),將數學成績進行分組,并根據各組人數制成如下頻率分布表:

(1)寫出![]() 的值,并估計本次考試全年級學生的數學平均分(同一組中的數據用該組區間的中點值作代表);
的值,并估計本次考試全年級學生的數學平均分(同一組中的數據用該組區間的中點值作代表);
(2)現從成績在![]() 內的學生中任選出兩名同學,從成績在
內的學生中任選出兩名同學,從成績在![]() 內的學生中任選一名同學,共三名同學參加學習習慣問卷調查活動.若
內的學生中任選一名同學,共三名同學參加學習習慣問卷調查活動.若![]() 同學的數學成績為43分,
同學的數學成績為43分,![]() 同學的數學成績為
同學的數學成績為![]() 分,求
分,求![]() 兩同學恰好都被選出的概率.
兩同學恰好都被選出的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com