
【題目】如圖,扇形OAB的半徑為1,圓心角為120°,四邊形PQRS是扇形的內接矩形,當其面積最大時,求點P的位置,并求此最大面積.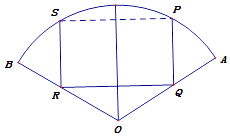
【答案】解:設SP中點為C,PQ中點為D,如圖所示;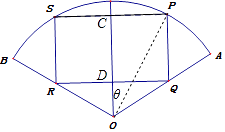
設∠COP=θ,則CP=1×sinθ=sinθ,
CO=cosθ,
DQ=CP=sinθ,
又∠DOQ= ![]() ,
,
∴OD= ![]() ,
,
∴CD=OC﹣OD=cosθ﹣ ![]() ,
,
∴S四邊形PQRS=CD×SP
=(cosθ﹣ ![]() )2sinθ
)2sinθ
=sin2θ﹣ ![]()
=sinθ﹣ ![]()
=sin2θ+ ![]() cos2θ﹣
cos2θ﹣ ![]()
= ![]() sin(2θ+
sin(2θ+ ![]() )﹣
)﹣ ![]() ,
,
當θ= ![]() 時,四邊形SPQR取得最大值為
時,四邊形SPQR取得最大值為
Smax= ![]() ,
,
此時點P在弧AB的四等分點處
【解析】根據題意,設SP中點為C,PQ中點為D,∠COP=θ,表示出四邊形SPRS的面積,再利用三角恒等變換求出它的最大值即可.
【考點精析】根據題目的已知條件,利用扇形面積公式的相關知識可以得到問題的答案,需要掌握若扇形的圓心角為![]() ,半徑為
,半徑為![]() ,弧長為
,弧長為![]() ,周長為
,周長為![]() ,面積為
,面積為![]() ,則
,則![]() ,
,![]() ,
,![]() .
.


科目:高中數學 來源: 題型:
【題目】
設函數![]()
(Ⅰ)若![]() 是函數
是函數![]() 的極值點,1和
的極值點,1和![]() 是
是![]() 的兩個不同零點,且
的兩個不同零點,且![]()
且![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若對任意![]() , 都存在
, 都存在![]() (
(![]() 為自然對數的底數),使得
為自然對數的底數),使得![]()
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解高三年級學生寒假期間的學習情況,某學校抽取了甲、乙兩班作為對象,調查這兩個班的學生在寒假期間平均每天學習的時間(單位:小時),統計結果繪成頻率分布直方圖(如圖).已知甲、乙兩班學生人數相同,甲班學生平均每天學習時間在區間![]() 的有8人.
的有8人.
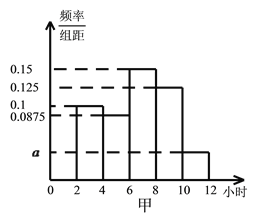

(I)求直方圖中![]() 的值及甲班學生平均每天學習時間在區間
的值及甲班學生平均每天學習時間在區間![]() 的人數;
的人數;
(II)從甲、乙兩個班平均每天學習時間大于10個小時的學生中任取4人參加測試,設4人中甲班學生的人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,圓C的參數方程為
中,圓C的參數方程為 ,(t為參數),在以原點O為極點,x軸的非負半軸為極軸建立的極坐標系中,直線
,(t為參數),在以原點O為極點,x軸的非負半軸為極軸建立的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() ,A,B兩點的極坐標分別為
,A,B兩點的極坐標分別為![]() .
.
(1)求圓C的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)點P是圓C上任一點,求△PAB面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為了了解全校學生的上網情況,在全校采取隨機抽樣的方法抽取了![]() 名學生(其中男女生人數恰好各占一半)進行問卷調查,并進行了統計,按男女分為兩組,再將每組學生的月上網次數分為
名學生(其中男女生人數恰好各占一半)進行問卷調查,并進行了統計,按男女分為兩組,再將每組學生的月上網次數分為![]() 組:
組: ![]() ,得到如圖所示的頻率分布直方圖:
,得到如圖所示的頻率分布直方圖:
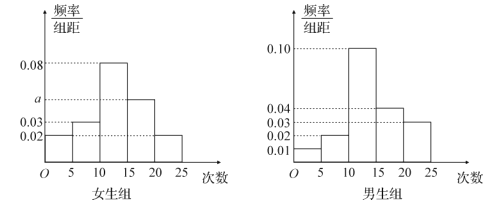
(1)寫出![]() 的值;
的值;
(2)求抽取的![]() 名學生中月上網次數不少于
名學生中月上網次數不少于![]() 次的學生的人數;
次的學生的人數;
(3)在抽取的![]() 名學生中,從月上網次數少于
名學生中,從月上網次數少于![]() 次的學生中隨機抽取
次的學生中隨機抽取![]() 人,求至少抽取到
人,求至少抽取到![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為 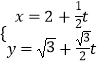 (t為參數).以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C1的極坐標方程為ρ=2.
(t為參數).以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C1的極坐標方程為ρ=2.
(1)若點M的直角坐標為(2, ![]() ),直線l與曲線C1交于A、B兩點,求|MA|+|MB|的值.
),直線l與曲線C1交于A、B兩點,求|MA|+|MB|的值.
(2)設曲線C1經過伸縮變換 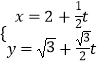 得到曲線C2 , 求曲線C2的內接矩形周長的最大值.
得到曲線C2 , 求曲線C2的內接矩形周長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校50名學生參加2015年全國數學聯賽初賽,成績全部介于90分到140分之間.將成績結果按如下方式分成五組:第一組![]() ,第二組
,第二組![]() ,…,第五組
,…,第五組![]() .按上述分組方法得到的頻率分布直方圖如圖所示.
.按上述分組方法得到的頻率分布直方圖如圖所示.
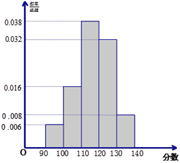
(1)若成績大于或等于100分且小于120分認為是良好的,求該校參賽學生在這次數學聯賽中成績良好的人數;
(2)若從第一、五組中共隨機取出兩個成績,記![]() 為取得第一組成績的個數,求
為取得第一組成績的個數,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com