Question

已知實數a≠b，試解關于x的不等式：．

Answer 1

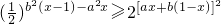
解：由于實數a≠b，關于x的不等式：，即≥，
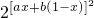
∴a²x-b²（x-1）≥[ac+b（1-x）²]²，
∴（a²-b²）x+b²≥a²x²+b²（1-x）²+2abx（1-x），
∴（a-b）²x≥（a-b）²x²，
∴x≥x²，解得 0≤x≤1，
故不等式的解集為[0，1]．
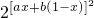
分析：不等式即≥，由此可得 a²x-b²（x-1）≥[ac+b（1-x）²]²，化簡為 （a-b）²x≥（a-b）²x²，即x≥x²，由此解得x的范圍
點評：本題主要考查復合函數的單調性的應用，指數不等式的解法，屬于中檔題．
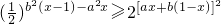