
【題目】已知數列![]() 中,
中,![]() ,點
,點![]() (
(![]() )在直線y = x上,
)在直線y = x上,
(Ⅰ)計算a2,a3,a4的值;
(Ⅱ)令bn=an+1﹣an﹣1,求證:數列{bn}是等比數列;
(Ⅲ)設Sn、Tn分別為數列{an}、{bn}的前n項和,是否存在實數λ,使得數列![]() 為等差數列?若存在,試求出λ的值;若不存在,請說明理由.
為等差數列?若存在,試求出λ的值;若不存在,請說明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)見解析;(Ⅲ)存在λ=2.
;(Ⅱ)見解析;(Ⅲ)存在λ=2.
【解析】試題分析:(1)根據點![]() 在直線
在直線![]() 上,可得
上,可得![]() ,代入計算可得
,代入計算可得![]() 的值;(2)利用
的值;(2)利用![]() ,及
,及![]() ,即可證明數列
,即可證明數列![]() 是等比數列;(3)求得數列的前三項,求得
是等比數列;(3)求得數列的前三項,求得![]() ,再驗證即可求得結論.
,再驗證即可求得結論.![]()
試題解析:(Ⅰ)由題意,∵點(n,2an+1﹣an)在直線y=x上,
∴2an+1﹣an=n
∵![]() ,∴
,∴![]() ,
,
同理,![]() ,
,![]() ;
;
(Ⅱ)證明:∵bn=an+1﹣an﹣1,2an+1﹣an=n
∴bn+1=an+2﹣an+1﹣1=![]() ﹣an+1﹣1=
﹣an+1﹣1=![]() (an+1﹣an﹣1)=
(an+1﹣an﹣1)=![]() bn,
bn,
∵b1=a2﹣a1﹣1=﹣![]()
∴數列{bn}是以﹣![]() 為首項,
為首項,![]() 為公比的等比數列;
為公比的等比數列;
(Ⅲ)解:存在λ=2,使數列![]() 是等差數列.
是等差數列.
由(Ⅱ)知,![]() ,
,![]() ,
,
∵an+1=n﹣1﹣bn=n﹣1+![]() ,∴an=n﹣2+
,∴an=n﹣2+![]() ,
,
∴Sn= =
=![]()
由題意,要使數列![]() 是等差數列,則
是等差數列,則![]()
∴2×![]() =
=![]() ﹣
﹣![]() λ+
λ+![]() ,∴λ=2
,∴λ=2
當λ=2時,![]() =
=![]() ,數列是等差數列
,數列是等差數列
∴當且僅當λ=2時,數列是等差數列.


 互動英語系列答案
互動英語系列答案 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案科目:高中數學 來源: 題型:
【題目】某企業準備投入適當的廣告費對產品進行促銷,在一年內預計銷售量Q(萬件)與廣告費x(萬元)之間的函數關系為Q=![]() (x>1),已知生產該產品的年固定投入為3萬元,每生產1萬件該產品另需再投入32萬元,若每件銷售價為“年平均每件生產成本(生產成本不含廣告費)的150%”與“年平均每件所占廣告費的50%”之和.
(x>1),已知生產該產品的年固定投入為3萬元,每生產1萬件該產品另需再投入32萬元,若每件銷售價為“年平均每件生產成本(生產成本不含廣告費)的150%”與“年平均每件所占廣告費的50%”之和.
(1)試將年利潤W(萬元)表示為年廣告費x(萬元)的函數;(年利潤=銷售收入-成本)
(2)當年廣告費為多少萬元時,企業的年利潤最大?最大年利潤為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產甲,乙兩種產品均需用![]() 兩種原料,已知生產1噸每種產品需用
兩種原料,已知生產1噸每種產品需用![]() 原料及每天原料的可用限額如下表所示,如果生產1噸甲,乙產品可獲利潤分別為3萬元、4萬元,則該企業可獲得最大利潤為__________萬元.
原料及每天原料的可用限額如下表所示,如果生產1噸甲,乙產品可獲利潤分別為3萬元、4萬元,則該企業可獲得最大利潤為__________萬元.
甲 | 乙 | 原料限額 | |
A(噸) | 3 | 2 | 12 |
B(噸) | 1 | 2 | 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是直線
是直線![]() 與橢圓
與橢圓![]() 的一個公共點,
的一個公共點,![]() 分別為該橢圓的左右焦點,設
分別為該橢圓的左右焦點,設![]() 取得最小值時橢圓為
取得最小值時橢圓為![]() .
.
(I)求橢圓![]() 的方程;
的方程;
(II)已知![]() 是橢圓
是橢圓![]() 上關于
上關于![]() 軸對稱的兩點,
軸對稱的兩點,![]() 是橢圓
是橢圓![]() 上異于
上異于![]() 的任意一點,直線
的任意一點,直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,試判斷
,試判斷![]() 是否為定值,并說明理由.
是否為定值,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直線![]() 的參數方程為
的參數方程為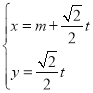 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,且曲線
,且曲線![]() 的左焦點
的左焦點![]() 在直線
在直線![]() 上.
上.
(1)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值;
的值;
(2)求曲線![]() 的內接矩形的周長的最大值.
的內接矩形的周長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圍建一個面積為360![]() 的矩形場地,要求矩形場地的一面利用舊墻(利用舊墻需維修),其它三面圍墻要新建,在舊墻的對面的新墻上要留一個寬度為2m的進出口,如圖所示,已知舊墻的維修費用為45元/m,新墻的造價為180元/m,設利用的舊墻的長度為
的矩形場地,要求矩形場地的一面利用舊墻(利用舊墻需維修),其它三面圍墻要新建,在舊墻的對面的新墻上要留一個寬度為2m的進出口,如圖所示,已知舊墻的維修費用為45元/m,新墻的造價為180元/m,設利用的舊墻的長度為![]() (單位:
(單位:![]() ),修建此矩形場地圍墻的總費用為
),修建此矩形場地圍墻的總費用為![]() (單位:元)
(單位:元)

(1)將![]() 表示為
表示為![]() 的函數;
的函數;
(2)試確定![]() ,使修建此矩形場地圍墻的總費用最小,并求出最小總費用。
,使修建此矩形場地圍墻的總費用最小,并求出最小總費用。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com