
將含有3n個正整數的集合M分成元素個數相等且兩兩沒有公共元素的三個集合A、B、C,其
中 ,
, ,
, ,若A、B、C中的元素滿足條件:
,若A、B、C中的元素滿足條件: ,
, ,
, 1,2,…,
1,2,…, ,則稱
,則稱 為“完并集合”.
為“完并集合”.
(1)若 為“完并集合”,則
為“完并集合”,則 的一個可能值為 .(寫出一個即可)
的一個可能值為 .(寫出一個即可)
(2)對于“完并集合” ,在所有符合條件的集合
,在所有符合條件的集合 中,其元素乘積最小的集合是 .
中,其元素乘積最小的集合是 .
(1)7、9、11中任一個;(2)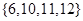 .
.
解析試題分析:(1)由題意, 分成元素個數相等且兩兩沒有公共元素的三個集合A、B、C,
分成元素個數相等且兩兩沒有公共元素的三個集合A、B、C,
設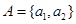 、
、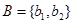 、
、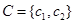 ,其中
,其中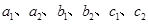 是
是 中的元素,
中的元素,
且互不相等.由定義可知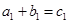 、
、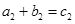 ,
,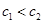 ,又它們都是正整數,所以
,又它們都是正整數,所以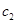 是
是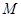 中最大的元
中最大的元
素.又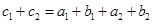 ,所以
,所以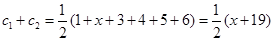 ,又
,又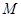 中元素為正整數,
中元素為正整數,
故 為正奇數.又由集合元素的互異性,
為正奇數.又由集合元素的互異性, 最小可為7,由
最小可為7,由 ,因為5+6=11可知
,因為5+6=11可知 最大可為11,
最大可為11,
否則就不存在兩個數的和等于 了.所以
了.所以 的一個可能值為7、9、11中任一個;(2)因為
的一個可能值為7、9、11中任一個;(2)因為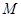 有12個元素,
有12個元素,
所以集合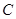 有4個元素,設
有4個元素,設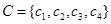 ,易知
,易知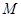 中元素之和為78,所以
中元素之和為78,所以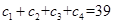 ,其中
,其中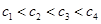 ,
,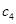 為
為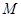 中最大元素,所以
中最大元素,所以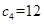 ,
,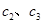 最大可分別取10、11,所以
最大可分別取10、11,所以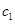 最小可等于
最小可等于
39-12-11-10=6,即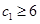 .所以集合
.所以集合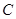 的所有可能的集合有:①
的所有可能的集合有:①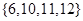 ②
②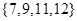 ③
③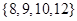
共三種,計算可知,元素乘積最小的集合為第①種——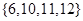 .
.
考點:新概念的理解、集合的含義


科目:高中數學 來源: 題型:填空題
給定集合 ,若對于任意
,若對于任意 ,都有
,都有 且
且 ,則稱集合
,則稱集合 為完美集合,給出下列四個論斷:①集合
為完美集合,給出下列四個論斷:①集合 是完美集合;②完美集合不能為單元素集;③集合
是完美集合;②完美集合不能為單元素集;③集合 為完美集合;④若集合
為完美集合;④若集合 為完美集合,則集合
為完美集合,則集合 為完美集合.
為完美集合.
其中正確論斷的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
對于E={a1,a2,….a100}的子集X={ ,
, ,…,
,…,  },定義X的“特征數列”
},定義X的“特征數列”
為x1,x2…,x100,其中 =
= =…=
=…= =1.其余項均為0,例如子集{a2,a3}的“特征數列”為0,1,0,0,…,0 子集{a1,a3,a5}的“特征數列”的前三項和等于________________;若E的子集P的“特征數列”P1,P2,…,P100滿足P1+Pi+1="1," 1≤i≤99;E 的子集Q的“特征數列” q1,q2,…,q100 滿足q1=1,q1+qj+1+qj+2=1,1≤j≤98,則P∩Q的元素個數為___________.
=1.其余項均為0,例如子集{a2,a3}的“特征數列”為0,1,0,0,…,0 子集{a1,a3,a5}的“特征數列”的前三項和等于________________;若E的子集P的“特征數列”P1,P2,…,P100滿足P1+Pi+1="1," 1≤i≤99;E 的子集Q的“特征數列” q1,q2,…,q100 滿足q1=1,q1+qj+1+qj+2=1,1≤j≤98,則P∩Q的元素個數為___________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com