
【題目】若實數x,y滿足x2-4xy+4y2+4x2y2=4,則當x+2y取得最大值時,![]() 的值為________.
的值為________.
【答案】2
【解析】
(解法1)因為實數x,y滿足x2-4xy+4y2+4x2y2=4,所以(x+2y)2+4x2y2-8xy=4,即(x+2y)2+4(xy-1)2=8,所以(x+2y)2=8-4(xy-1)2,所以當(xy-1)2=0時,即xy=1時,x+2y取得最大值,此時x=![]() ,y=
,y=![]() ,所以
,所以![]() =2.(解法2)因為實數x,y滿足x2-4xy+4y2+4x2y2=4,所以(x-2y)2+4x2y2=4,令x-2y=2cosθ,xy=sinθ,則(x+2y)2=(x-2y)2+8xy=4cos2θ+8sinθ,所以(x+2y)2=-4sin2θ+8sinθ+4,所以當sinθ=1時,(x+2y)2取得最大值,此時xy=1,x-2y=0,所以
=2.(解法2)因為實數x,y滿足x2-4xy+4y2+4x2y2=4,所以(x-2y)2+4x2y2=4,令x-2y=2cosθ,xy=sinθ,則(x+2y)2=(x-2y)2+8xy=4cos2θ+8sinθ,所以(x+2y)2=-4sin2θ+8sinθ+4,所以當sinθ=1時,(x+2y)2取得最大值,此時xy=1,x-2y=0,所以![]() =2.
=2.


科目:高中數學 來源: 題型:
【題目】已知中心在原點,焦點在x軸上的橢圓,離心率![]() ,且經過拋物線
,且經過拋物線![]() 的焦點.若過點
的焦點.若過點![]() 的直線
的直線![]() 斜率不等于零
斜率不等于零![]() 與橢圓交于不同的兩點E、
與橢圓交于不同的兩點E、![]() 在B、F之間
在B、F之間![]() ,
,
![]() 求橢圓的標準方程;
求橢圓的標準方程;
![]() 求直線l斜率的取值范圍;
求直線l斜率的取值范圍;
![]() 若
若![]() 與
與![]() 面積之比為
面積之比為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】英國統計學家E.H.辛普森1951年提出了著名的辛普森悖論,下面這個案例可以讓我們感受到這個悖論.有甲乙兩名法官,他們都在民事庭和行政庭主持審理案件,他們審理的部分案件被提出上訴.記錄這些被上述案件的終審結果如下表所示(單位:件):
法官甲 | 法官乙 | ||||||
終審結果 | 民事庭 | 行政庭 | 合計 | 終審結果 | 民事庭 | 行政庭 | 合計 |
維持 | 29 | 100 | 129 | 維持 | 90 | 20 | 110 |
推翻 | 3 | 18 | 21 | 推翻 | 10 | 5 | 15 |
合計 | 32 | 118 | 150 | 合計 | 100 | 25 | 125 |
記甲法官在民事庭、行政庭以及所有審理的案件被維持原判的比率分別為![]() ,
,![]() 和
和![]() ,記乙法官在民事庭、行政庭以及所有審理的案件被維持原判的比率分別為
,記乙法官在民事庭、行政庭以及所有審理的案件被維持原判的比率分別為![]() ,
,![]() 和
和![]() ,則下面說法正確的是
,則下面說法正確的是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]()
C. ![]() ,
,![]() ,
,![]() D.
D. ![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,焦點為
上,焦點為![]() ,圓O的直徑為
,圓O的直徑為![]() .
.

(1)求橢圓C及圓O的標準方程;
(2)設直線l與圓O相切于第一象限內的點P,且直線l與橢圓C交于![]() 兩點.記
兩點.記![]() 的面積為
的面積為![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 的中點為
的中點為![]() .
.
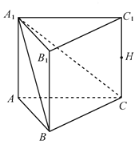
(Ⅰ)求證:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國已進入新時代中國特色社會主義時期,人民生活水平不斷提高.某市隨機統計了城區若干戶市民十月人均生活支出比九月人均生活支出增加量(記為P元)的情況,并根據統計數據制成如圖頻率分布直方圖.
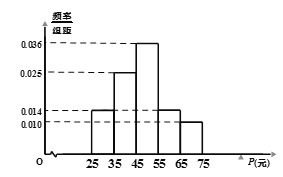
(1)根據頻率分布直方圖估算P的平均值![]() ;
;
(2)若該市城區有4戶市民十月人均生活支出比九月人均生活支出分別增加了42元,50元,52元,60元,從這4戶中隨機抽取2戶,求這2戶P值的和超過100元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某條公共汽車線路收支差額![]() 與乘客量
與乘客量![]() 的函數關系如下圖所示(收支差額=車票收入-支出費用),由于目前本條線路虧損,公司有關人員提出了兩條建議:建議(1)不改變車票價格,減少支出費用;建議(2)不改變支出費用,提高車票價格.下面給出的四個圖形中,實線和虛線分別表示目前和建議后的函數關系,則( )
的函數關系如下圖所示(收支差額=車票收入-支出費用),由于目前本條線路虧損,公司有關人員提出了兩條建議:建議(1)不改變車票價格,減少支出費用;建議(2)不改變支出費用,提高車票價格.下面給出的四個圖形中,實線和虛線分別表示目前和建議后的函數關系,則( )

A.①反映建議(2),③反映建議(1)B.①反映建議(1),③反映建議(2)
C.②反映建議(1),④反映建議(2)D.④反映建議(1),②反映建議(2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 的前
的前![]() 項和為
項和為![]() 且滿足
且滿足![]() ,
,![]() (
(![]() 為常數,
為常數,![]() ).
).
(1)求![]() ;
;
(2)若數列![]() 是等比數列,求實數
是等比數列,求實數![]() 的值;
的值;
(3)是否存在實數![]() ,使得數列
,使得數列![]() 滿足:可以從中取出無限多項并按原來的先后次序排成一個等差數列?若存在,求出所有滿足條件的值;若不存在,請說明理由.
滿足:可以從中取出無限多項并按原來的先后次序排成一個等差數列?若存在,求出所有滿足條件的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 為信號源點,
為信號源點,![]() 、
、![]() 、
、![]() 是三個居民區,已知
是三個居民區,已知![]() 、
、![]() 都在
都在![]() 的正東方向上,
的正東方向上,![]() ,
,![]() ,
,![]() 在
在![]() 的北偏西45°方向上,
的北偏西45°方向上,![]() ,現要經過點
,現要經過點![]() 鋪設一條總光纜直線
鋪設一條總光纜直線![]() (
(![]() 在直線
在直線![]() 的上方),并從
的上方),并從![]() 、
、![]() 、
、![]() 分別鋪設三條最短分支光纜連接到總光纜
分別鋪設三條最短分支光纜連接到總光纜![]() ,假設鋪設每條分支光纜的費用與其長度的平方成正比,比例系數為1元/
,假設鋪設每條分支光纜的費用與其長度的平方成正比,比例系數為1元/![]() ,設
,設![]() ,(
,(![]() ),鋪設三條分支光纜的總費用為
),鋪設三條分支光纜的總費用為![]() (元).
(元).
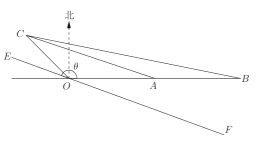
(1)求![]() 關于
關于![]() 的函數表達式;
的函數表達式;
(2)求![]() 的最小值及此時
的最小值及此時![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com