Question

定義：對于各項均為整數的數列，如果(=1，2，3， )為完全平方數，則稱數列具有“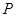性質”；不論數列是否具有“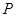性質”，如果存在數列與不是同一數列，且滿足下面兩個條件：

（1）是的一個排列；

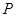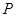（2）數列具有“性質”，則稱數列具有“變換性質”．

給出下面三個數列：

①數列的前項和；

②數列：1，2，3，4，5；

③數列：1，2，3，4，5，6，7，8，9，10，11.

具有“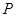性質”的為        ；具有“變換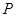性質”的為           .

 

Answer 1

【答案】

①、②

【解析】

試題分析：對于①，求出數列{a_n}的通項，驗證a_i+i=i²（i=1，2，3，…）為完全平方數，可得結論；對于②，數列1，2，3，4，5，具有“變換P性質”，數列{b_n}為3，2，1，5，4，具有“P性質”；對于③，因為11，4都只有與5的和才能構成完全平方數，所以1，2，3，…，11，不具有“變換P性質”． 解：對于①，當n≥2時，a_n=S_n-S_n-1=n²-n，∵a₁=0，∴a_n=n²-n，∴a_i+i=i²（i=1，2，3，…）為完全平方數，∴數列{a_n}具有“P性質”；，對于②，數列1，2，3，4，5，具有“變換P性質”，數列{b_n}為3，2，1，5，4，具有“P性質”，∴數列{a_n}具有“變換P性質”；，對于③，因為11，4都只有與5的和才能構成完全平方數，所以1，2，3，…，11，不具有“變換P性質”．，故答案為：①，②．

考點：新定義

點評：本題考查新定義，考查學生分析解決問題的能力，正確理解新定義是關鍵．