
如圖,⊙O的半徑OB垂直于直徑AC,M為AO上一點,BM的延長線交⊙O于N,過N點的切線交CA的延長線于P.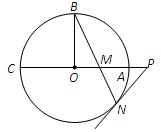
(1)求證:PM2=PA•PC;
(2)若⊙O的半徑為2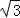 ,OA=
,OA=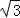 OM,求MN的長.
OM,求MN的長.
(1)(1)做出輔助線連接ON,根據切線得到直角,根據垂直得到直角,即∠ONB+∠BNP=90°且∠OBN+∠BMO=90°,根據同角的余角相等,得到角的相等關系,得到結論.
(2)MN=2
解析試題分析:證明:連接ON,因為PN切⊙O于N,
∴∠ONP=90°,
∴∠ONB+∠BNP=90°
∵OB=ON,
∴∠OBN=∠ONB
因為OB⊥AC于O,
∴∠OBN+∠BMO=90°,
故∠BNP=∠BMO=∠PMN,PM=PN
∴PM2=PN2=PA•PC
(2)∵OM=2,BO=2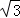 ,BM=4
,BM=4
∵BM•MN=CM•MA=(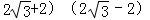 (2
(2 )=8,
)=8,
∴MN=2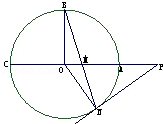
考點:與圓有關的比例線段
點評:本題要求證明一個PM2=PA•PC結論,實際上這是一個名叫切割線定理的結論,可以根據三角形相似對應邊成比例來證明,這是一個基礎題.


科目:高中數學 來源: 題型:解答題
如圖所示,已知PA與⊙O相切,A為切點,過點P的割線交圓于B、C兩點,弦CD∥AP,AD、BC相交于點E,F為CE上一點,且DE2 = EF·EC.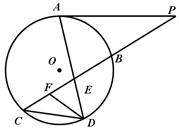
(Ⅰ)求證:CE·EB = EF·EP;
(Ⅱ)若CE:BE = 3:2,DE = 3,EF = 2,求PA的長.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,AB是⊙O的直徑 ,AC是弦 ,∠BAC的平分線AD交⊙O于點D,DE⊥AC,交AC的延長線于點E.OE交AD于點F.
(Ⅰ)求證:DE是⊙O的切線;
(Ⅱ)若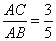 ,求
,求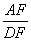 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖AB為圓O直徑,P為圓O外一點,過P點作PC⊥AB,垂是為C,PC交圓O于D點,PA交圓O于E點,BE交PC于F點。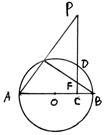
(I)求證:∠PFE=∠PAB (II)求證:CD2=CF·CP
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(10分)如圖,A,B,C,D四點在同一圓上,AD的延長線與BC的延長線交于E點,且EC=ED。
(1)證明:CD//AB;(2)延長CD到F,延長DC到G,使得EF=EG,證明:A,B,G,F四點共圓。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com