Question

設方程x³-3x=k有3個不等的實根，則常數k的取值范圍是________．

Answer 1

（-2，2）
分析：利用導數，判斷出函數的極值點，用極值解決根的存在與個數問題．
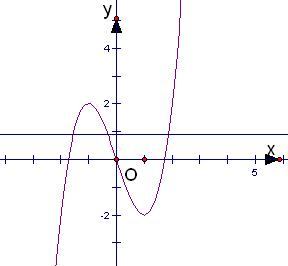
解答：解：設f（x）=x³-3x，
對函數求導，f′（x）=3x²-3=0，x=-1，1．
x＜-1時，f（x）單調增，-1＜x＜1時，單調減，x＞1時，單調增，
要有三個不等實根，則f（-1）=-1+3-k＞0且f（1）=1-3-k＜0．
解得-2＜k＜2
故答案為：（-2，2）．
點評：學會用導數及單調性處理根的存在與個數問題，極值的正負是解決此問題的關鍵．是中檔題．