
【題目】已知函數f (x)=![]() (a≠0).
(a≠0).
(1)當a=-1,b=0時,求函數f (x)的極值;
(2)當b=1時,若函數f (x)沒有零點,求實數a的取值范圍.
【答案】(1)極小值為![]() ,無極大值; (2)
,無極大值; (2)![]() .
.
【解析】
(1)當![]() 時,求得函數的導數,利用導數求得函數的單調性,結合函數極值的定義,即可求解;
時,求得函數的導數,利用導數求得函數的單調性,結合函數極值的定義,即可求解;
(2)把函數![]() 沒有零點,轉化為方程ax-a+ex=0無實根,令
沒有零點,轉化為方程ax-a+ex=0無實根,令![]() ,利用導數求得函數
,利用導數求得函數![]() 的單調性與最值,列出不等式,即可求解.
的單調性與最值,列出不等式,即可求解.
(1)當![]() 時,函數
時,函數![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() 單調遞增.
單調遞增.
所以![]() 的極小值為
的極小值為![]() ,無極大值.
,無極大值.
(2)當![]() 時,函數
時,函數![]() ,
,
因為函數![]() 沒有零點,即方程
沒有零點,即方程![]() 無實根,即ax-a+ex=0無實根,
無實根,即ax-a+ex=0無實根,
令![]() ,則
,則![]() ,
,
若![]() 時,則
時,則![]() 在R上單調遞增,
在R上單調遞增,![]() 此時存在
此時存在![]() ,使得
,使得![]() ,不合題意;
,不合題意;
若![]() 時,令
時,令![]() ,即
,即![]() ,得
,得![]() ;
;
令![]() ,得
,得![]() ,
,
所以當![]() ,函數
,函數![]() 取得最小值,最小值為
取得最小值,最小值為![]() ,
,
![]() 要使得函數
要使得函數![]() 沒有零點,則滿足
沒有零點,則滿足![]() ,即
,即![]() ,
,
解得![]() ,
,
綜上所述,實數的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】某商場為提高服務質量,隨機調查了50名男顧客和50名女顧客,每位顧客對該商場的服務給出滿意或不滿意的評價,得到下面列聯表:
滿意 | 不滿意 | |
男顧客 | 40 | 10 |
女顧客 | 30 | 20 |
(1)分別估計男、女顧客對該商場服務滿意的概率;
(2)能否有![]() 的把握認為男、女顧客對該商場服務的評價有差異?
的把握認為男、女顧客對該商場服務的評價有差異?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市工業部門計劃對所轄中小型企業推行節能降耗技術改造,下面是對所轄企業是否支持技術改造進行的問卷調查的結果:
支持 | 不支持 | 合計 | |
中型企業 | 40 | ||
小型企業 | 240 | ||
合計 | 560 |
已知從這560家企業中隨機抽取1家,抽到支持技術改造的企業的概率為![]() .
.
(1)能否在犯錯誤的概率不超過0.025的前提下認為“是否支持節能降耗技術改造”與“企業規模”有關?
(2)從支持節能降耗的中小企業中按分層抽樣的方法抽出8家企業,然后從這8家企業選出2家進行獎勵,分別獎勵中型企業20萬元,小型企業10萬元.求獎勵總金額為20萬元的概率.
附:![]()
| 0.05 | 0.025 | 0.01 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校高三年級有400名學生參加某項體育測試,根據男女學生人數比例,使用分層抽樣的方法從中抽取了100名學生,記錄他們的分數,將數據分成7組:![]() ,整理得到如下頻率分布直方圖:
,整理得到如下頻率分布直方圖:
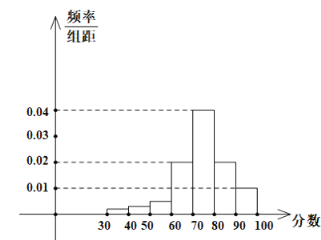
(1)若該樣本中男生有55人,試估計該學校高三年級女生總人數;
(2)若規定小于60分為“不及格”,從該學校高三年級學生中隨機抽取一人,估計該學生不及格的概率;
(3)若規定分數在![]() 為“良好”,
為“良好”,![]() 為“優秀”.用頻率估計概率,從該校高三年級隨機抽取三人,記該項測試分數為“良好”或“優秀”的人數為X,求X的分布列和數學期望.
為“優秀”.用頻率估計概率,從該校高三年級隨機抽取三人,記該項測試分數為“良好”或“優秀”的人數為X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD為平行四邊形,四邊形ADEF是正方形,且BD⊥平面CDE,H是BE的中點,G是AE,DF的交點.

(1)求證:GH∥平面CDE;
(2)求證:面ADEF⊥面ABCD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的偶函數f(x)和奇函數g(x)滿足![]() .
.
(1)求函數f(x)和g(x)的表達式;
(2)當![]() 時,不等式
時,不等式![]() 恒成立,求實數a的取值范圍;
恒成立,求實數a的取值范圍;
(3)若方程![]() 在
在![]() 上恰有一個實根,求實數m的取值范圍.
上恰有一個實根,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】交通部門調查在高速公路上的平均車速情況,隨機抽查了60名家庭轎車駕駛員,統計其中有40名男性駕駛員,其中平均車速超過![]() 的有30人,不超過
的有30人,不超過![]() 的有10人;在其余20名女性駕駛員中,平均車速超過
的有10人;在其余20名女性駕駛員中,平均車速超過![]() 的有5人,不超過
的有5人,不超過![]() 的有15人.
的有15人.
(1)完成下面的![]() 列聯表,并據此判斷是否有
列聯表,并據此判斷是否有![]() 的把握認為,家庭轎車平均車速超過
的把握認為,家庭轎車平均車速超過![]() 與駕駛員的性別有關;
與駕駛員的性別有關;
平均車速超過 | 平均車速不超過 | 合計 | |
男性駕駛員 | |||
女性駕駛員 | |||
合計 |
(2)根據這些樣本數據來估計總體,隨機調查3輛家庭轎車,記這3輛車中,駕駛員為女性且平均車速不超過![]() 的人數為
的人數為![]() ,假定抽取的結果相互獨立,求
,假定抽取的結果相互獨立,求![]() 的分布列和數學期望.
的分布列和數學期望.
參考公式: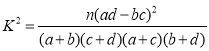
![]()
臨界值表:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com