
在四棱錐P-ABCD中,底面ABCD是a的正方形,PA⊥平面ABCD,且PA=2AB
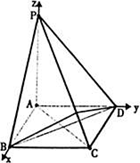
(Ⅰ)求證:平面PAC⊥平面PBD;
(Ⅱ)求二面角B-PC-D的余弦值.
|
解:(Ⅰ)證明:∵PA⊥平面ABCD ∴PA⊥BD ∵ABCD為正方形 ∴AC⊥BD ∴BD⊥平面PAC又BD在平面BPD內(nèi),∴平面PAC⊥平面BPD 6分 (Ⅱ)解法一:在平面BCP內(nèi)作BN⊥PC垂足為N,連DN, ∵Rt△PBC≌Rt△PDC,由BN⊥PC得DN⊥PC; ∴∠BND為二面角B-PC-D的平面角,在△BND中, BN=DN= ∴cos∠BND= 解法二:以A為原點(diǎn),AB、AD、AP所在直線分別為x軸、y軸、z軸建立空間坐標(biāo)系如圖,
在平面BCP內(nèi)作BN⊥PC垂足為N連DN, ∵Rt△PBC≌Rt△PDC,由BN⊥PC得DN⊥PC;∴∠BND為二面角B-PC-D的平面角 設(shè) 解法三:以A為原點(diǎn),AB、AD、AP所在直線分別為x軸、y軸、z軸建立如圖空間坐標(biāo)系,
作AM⊥PB于M、AN⊥PD于N,易證AM⊥平面PBC,AN⊥平面PDC, 設(shè) ∵二面角B-PC-D的平面角與∠MAN互補(bǔ) ∴二面角B-PC-D的余弦值為 |



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 已知在四棱錐P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,
已知在四棱錐P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 如圖.在四棱錐P一ABCD中,底面ABCD是正方形,側(cè)棱PD⊥底 面ABCD,PD=DC=2,E是PC的中點(diǎn).
如圖.在四棱錐P一ABCD中,底面ABCD是正方形,側(cè)棱PD⊥底 面ABCD,PD=DC=2,E是PC的中點(diǎn).查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 已知在四棱錐P一ABCD中,二面角P一AD一B為60°,∠PDA=45°,∠DAB=90°,∠PAD=90°,∠ADC=135°,
已知在四棱錐P一ABCD中,二面角P一AD一B為60°,∠PDA=45°,∠DAB=90°,∠PAD=90°,∠ADC=135°,查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 如圖,在四棱錐P一ABCD中,底面ABCD為菱形,∠BAD=60°,Q為AD的中點(diǎn).PA=PD=AD=2,點(diǎn)M在線段PC上 PM=
如圖,在四棱錐P一ABCD中,底面ABCD為菱形,∠BAD=60°,Q為AD的中點(diǎn).PA=PD=AD=2,點(diǎn)M在線段PC上 PM=| 1 | 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 (本小題滿分14分)在四棱錐P-ABCD中,底面ABCD是正方形,側(cè)棱PD與底面ABCD垂直,PD=DC,E是PC的中點(diǎn),作EF
(本小題滿分14分)在四棱錐P-ABCD中,底面ABCD是正方形,側(cè)棱PD與底面ABCD垂直,PD=DC,E是PC的中點(diǎn),作EF![]() 于點(diǎn)F(Ⅰ)證明PA
于點(diǎn)F(Ⅰ)證明PA![]() 平面EBD.
平面EBD.
(Ⅱ)證明PB![]() 平面EFD.
平面EFD.
(Ⅲ)求二面角![]() 的余弦值;
的余弦值;
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com