
【題目】某教育機構隨機某校20個班級,調查各班關注漢字聽寫大賽的學生人數,根據所得數據的莖葉圖,以組距為5將數據分組成[0,5),[5,10),[10,15),[15,20),[20,25),[25,30),[30,35),[35,40]時,所作的頻率分布直方圖如圖所示,則原始莖葉圖可能是( ) 
A.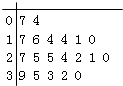
B.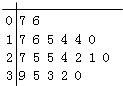
C.
D.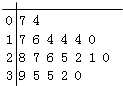
 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案 課堂練加測系列答案
課堂練加測系列答案 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,在梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 是矩形,
是矩形, ![]() ,點
,點![]() 在線段
在線段![]() 上.
上.
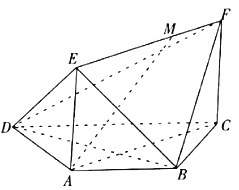
(1)當![]() 為何值時,
為何值時, ![]() 平面
平面![]() ?證明你的結論;
?證明你的結論;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產一種儀器的元件,由于受生產能力和技術水平的限制,會產生一些次品,根據經驗知道,其次品率P與日產量x(萬件)之間大體滿足關系: 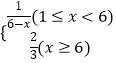 .(注:次品率=次品數/生產量,如P=0.1表示每生產10件產品,有1件為次品,其余為合格品).已知每生產1萬件合格的元件可以盈利2萬元,但每生產1萬件次品將虧損1萬元,故廠方希望定出合適的日產量.
.(注:次品率=次品數/生產量,如P=0.1表示每生產10件產品,有1件為次品,其余為合格品).已知每生產1萬件合格的元件可以盈利2萬元,但每生產1萬件次品將虧損1萬元,故廠方希望定出合適的日產量.
(1)試將生產這種儀器的元件每天的盈利額T(萬元)表示為日產量x(萬件)的函數;
(2)當日產量x為多少時,可獲得最大利潤?
查看答案和解析>>
科目:高中數學 來源: 題型:
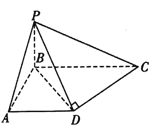
【題目】如圖,在四棱錐![]() 中,已知
中,已知![]() 底面
底面![]() ,異面直線
,異面直線![]() 和
和![]() 所成角等于
所成角等于![]() .
.
(1)求證: 平面![]() 平面
平面![]() ;
;
(2)求直線![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(3) 在棱![]() 上是否存在一點
上是否存在一點![]() ,使得平面
,使得平面![]() 與平面
與平面![]() 所成銳二面角的正切值為
所成銳二面角的正切值為![]() ?若存在,指出點
?若存在,指出點![]() 在棱
在棱![]() 上的位置,若不存在,說明理由.
上的位置,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國內某知名連鎖店分店開張營業期間,在固定的時間段內消費達到一定標準的顧客可進行一次抽獎活動,隨著抽獎活動的有效開展,參與抽獎活動的人數越來越多,該分店經理對開業前![]() 天參加抽獎活動的人數進行統計,
天參加抽獎活動的人數進行統計, ![]() 表示開業第
表示開業第![]() 天參加抽獎活動的人數,得到統計表格如下:
天參加抽獎活動的人數,得到統計表格如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
經過進一步統計分析,發現![]() 與
與![]() 具有線性相關關系.
具有線性相關關系.
(1)若從這![]() 天中隨機抽取兩天,求至少有
天中隨機抽取兩天,求至少有![]() 天參加抽獎人數超過
天參加抽獎人數超過![]() 的概率;
的概率;
(2)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并估計若該活動持續
,并估計若該活動持續![]() 天,共有多少名顧客參加抽獎.
天,共有多少名顧客參加抽獎.
參考公式: 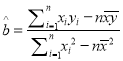 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|< ![]() )的部分圖象如圖所示.
)的部分圖象如圖所示. 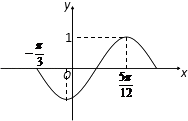
(1)求f(x)> ![]() 在x∈[0,π]上的解集;
在x∈[0,π]上的解集;
(2)設g(x)=2 ![]() cos2x+f(x),g(α)=
cos2x+f(x),g(α)= ![]() +
+ ![]() ,α∈(
,α∈( ![]() ,
, ![]() ),求sin2α的值.
),求sin2α的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國內某知名連鎖店分店開張營業期間,在固定的時間段內消費達到一定標準的顧客可進行一次抽獎活動,隨著抽獎活動的有效開展,參與抽獎活動的人數越來越多,該分店經理對開業前![]() 天參加抽獎活動的人數進行統計,
天參加抽獎活動的人數進行統計, ![]() 表示開業第
表示開業第![]() 天參加抽獎活動的人數,得到統計表格如下:
天參加抽獎活動的人數,得到統計表格如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
經過進一步統計分析,發現![]() 與
與![]() 具有線性相關關系.
具有線性相關關系.
(1)根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若該分店此次抽獎活動自開業始,持續![]() 天,參加抽獎的每位顧客抽到一等獎(價值
天,參加抽獎的每位顧客抽到一等獎(價值![]() 元獎品)的概率為
元獎品)的概率為![]() ,抽到二等獎(價值
,抽到二等獎(價值![]() 元獎品)的概率為
元獎品)的概率為![]() ,抽到三等獎(價值
,抽到三等獎(價值![]() 元獎品)的概率為
元獎品)的概率為![]() .
.
試估計該分店在此次抽獎活動結束時送出多少元獎品?
參考公式: 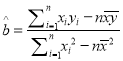 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 的參數方程是
的參數方程是 (
(![]() 是參數),以坐標原點為原點,
是參數),以坐標原點為原點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)判斷直線![]() 與曲線
與曲線![]() 的位置關系;
的位置關系;
(2)過直線![]() 上的點作曲線
上的點作曲線![]() 的切線,求切線長的最小值.
的切線,求切線長的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com