已知一口袋中共有4只白球和2只紅球
(1)從口袋中一次任取4只球,取到一只白球得1分,取到一只紅球得2分,設得分為隨機變量X,求X的分布列與數學期望;
(2)從口袋中每次取一球,取后放回,直到連續出現兩次白球就停止取球,求6次取球后恰好被停止的概率.
【答案】
分析:(1)根據題意可得:X的可能取值為4、5、6,再分別求出其復數的概率,即可得到X的分布列,進而得到其數學期望.
(2)設“6次取球后恰好被停止”為事件A,后面兩次一定是白球,前面4次可以出現白球,只要保證出現的白球不連續出現2次并且與后面的白球也不連續即可.
解答:解:(1)根據題意可得:X的可能取值為4、5、6.
所以P(X=4)=
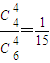
P(X=5)=
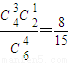
P(X=6)=
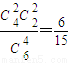
屬于X的分布列為:
屬于X的數學期望為:
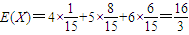
5分
(2)設“6次取球后恰好被停止”為事件A
則
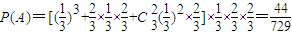
∴6次取球后恰好被停止的概率為
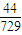
.(10分)
點評:解決此類問題的關鍵是熟練掌握離散型隨機變量的分布列與數學期望,以及等可能事件的概率,考查學生的分析問題、解決問題的能力.

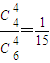
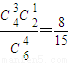
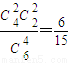
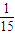
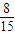
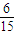
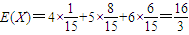 5分
5分 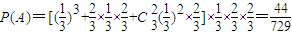
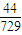 .(10分)
.(10分)

 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案 黃岡海淀全程培優測試卷系列答案
黃岡海淀全程培優測試卷系列答案