解:由已知有f'(x)=lnx+1,
令f'(x)=0,即lnx+1=0,解得x=

.當x
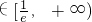
時,f'(x)≥0,即f(x)在
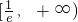
上是增函數;
當x
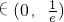
時,f'(x)<0,即f(x)在

上是減函數.(4分)
于是由b≥

,有f(b)≥f(

),即blnb≥
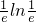
.
整理得
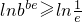
∴
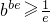
.(6分)
(2)F'(x)=f'(x)+(a-1)=lnx+a,令F'(x)=0,即lnx+a=0,
解得x=e
-a.當e
-a≤1,即a≥0時,F(x)在[1,+∞)上是增函數,
∴F(x)
min=F(1)=a-1;
當e
-a>1,即a<0時,F(x)在[1,e
-a]上是減函數,在(e
-a,+∞)上是增函數,
∴F(x)
min=F(e
-a)=e
-alne
-a+(a-1)e
-a=-e
-a.
即F(x)存在最小值,當a≥0時,最小值為a-1,當a<0時,最小值為-e
-a.(12分)
分析:(1)先對函數求導,研究函數的單調區間,由b≥e結合函數的單調性可得f(b)≥f(e),整理可得
(2)對函數F(x)求導,找出該函數的極值點x=e
-a,討論e
-a與1的大小,確定F(x)在區間[1,+∞)上的單調性,判斷函數F((x)是否存在最小值
點評:本題考查了導數的應用:利用導數判斷函數的單調性及求單調區間;函數在區間上的最值的求解,其一般步驟是:先求極值,比較函數在區間內所有極值與端點函數.若函數在區間上有唯一的極大(小)值,則該極值就是相應的最大(小)值.

 ,求證
,求證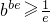 (e是自然對數的底數);
(e是自然對數的底數); .當x
.當x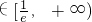 時,f'(x)≥0,即f(x)在
時,f'(x)≥0,即f(x)在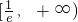 上是增函數;
上是增函數;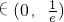 時,f'(x)<0,即f(x)在
時,f'(x)<0,即f(x)在 上是減函數.(4分)
上是減函數.(4分) ,有f(b)≥f(
,有f(b)≥f( ),即blnb≥
),即blnb≥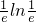 .
.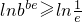
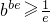 .(6分)
.(6分)

 已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<