
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)令![]() 在
在![]() 上最小值為
上最小值為![]() ,證明:
,證明:![]() .
.
【答案】(1)![]() ;(2)見解析.
;(2)見解析.
【解析】
(1)將![]() 轉(zhuǎn)化為
轉(zhuǎn)化為![]() 對任意
對任意![]() 恒成立,令
恒成立,令![]() ,故只需
,故只需![]() ,即可求出
,即可求出![]() 的值;
的值;
(2)由(1)知![]() ,可得
,可得![]() ,令
,令![]() ,可證
,可證![]() ,使得
,使得![]() ,從而可確定
,從而可確定![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,進而可得
上單調(diào)遞增,進而可得![]() ,即
,即![]() ,即可證出
,即可證出![]()
![]()
![]() .
.
函數(shù)![]() 的定義域為
的定義域為![]() ,因為
,因為![]() 對任意
對任意![]() 恒成立,
恒成立,
即![]() 對任意
對任意![]() 恒成立,
恒成立,
令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,故
,故![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
又![]() ,所以當
,所以當![]() 時,
時,![]() ,不符合題意;
,不符合題意;
當![]() 時,令
時,令![]() 得
得![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,
上單調(diào)遞減,
所以![]() ,
,
所以要使![]() 在
在![]() 時恒成立,則只需
時恒成立,則只需![]() ,即
,即![]() ,
,
令![]() ,
,![]() ,
,
所以![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 單調(diào)遞減,在
單調(diào)遞減,在![]() 上單調(diào)遞增,所以
上單調(diào)遞增,所以![]() ,
,
即![]() ,又
,又![]() ,所以
,所以![]() ,
,
故滿足條件的![]() 的值只有
的值只有![]()
(2)由(1)知![]() ,所以
,所以![]() ,
,
令![]() ,則
,則![]() ,
,
當![]() ,時
,時![]() ,即
,即![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
又![]() ,
,![]() ,所以
,所以![]() ,使得
,使得![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
即![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,且
上單調(diào)遞增,且![]()
所以![]() ,
,
即![]() ,所以
,所以![]() ,即
,即![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中數(shù)學 來源: 題型:
【題目】2019年7月,中國良渚古城遺址獲準列入世界遺產(chǎn)名錄,標志著中華五千年文明史得到國際社會認可.良渚古城遺址是人類早期城市文明的范例,實證了中華五千年文明史.考古科學家在測定遺址年齡的過程中利用了“放射性物質(zhì)因衰變而減少”這一規(guī)律.已知樣本中碳14的質(zhì)量N隨時間T(單位:年)的衰變規(guī)律滿足![]() (
(![]() 表示碳14原有的質(zhì)量),則經(jīng)過5730年后,碳14的質(zhì)量變?yōu)樵瓉淼?/span>______;經(jīng)過測定,良渚古城遺址文物樣本中碳14的質(zhì)量是原來的
表示碳14原有的質(zhì)量),則經(jīng)過5730年后,碳14的質(zhì)量變?yōu)樵瓉淼?/span>______;經(jīng)過測定,良渚古城遺址文物樣本中碳14的質(zhì)量是原來的![]() 至
至![]() ,據(jù)此推測良渚古城存在的時期距今約在5730年到______年之間.(參考數(shù)據(jù):
,據(jù)此推測良渚古城存在的時期距今約在5730年到______年之間.(參考數(shù)據(jù):![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在貫徹中共中央、國務(wù)院關(guān)于精準扶貧政策的過程中,某單位在某市定點幫扶甲、乙兩村各![]() 戶貧困戶.為了做到精準幫扶,工作組對這
戶貧困戶.為了做到精準幫扶,工作組對這![]() 戶村民的年收入情況、勞動能力情況.子女受教育情況、危舊房情況、患病情況等進行調(diào)查.并把調(diào)查結(jié)果轉(zhuǎn)化為各戶的貧困指標
戶村民的年收入情況、勞動能力情況.子女受教育情況、危舊房情況、患病情況等進行調(diào)查.并把調(diào)查結(jié)果轉(zhuǎn)化為各戶的貧困指標![]() .將指標
.將指標![]() 按照
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
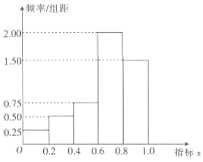
,![]() 分成五組,得到如圖所示的頻率分布直方圖.規(guī)定若
分成五組,得到如圖所示的頻率分布直方圖.規(guī)定若![]() ,則認定該戶為“絕對貧困戶”,否則認定該戶為“相對貧困戶”,且當
,則認定該戶為“絕對貧困戶”,否則認定該戶為“相對貧困戶”,且當![]() 時,認定該戶為“低收入戶”;當
時,認定該戶為“低收入戶”;當![]() 時,認定該戶為“亟待幫助戶".已知此次調(diào)查中甲村的“絕對貧困戶”占甲村貧困戶的
時,認定該戶為“亟待幫助戶".已知此次調(diào)查中甲村的“絕對貧困戶”占甲村貧困戶的![]() .
.
(1)完成下面的列聯(lián)表,并判斷是否有![]() 的把握認為絕對貧困戶數(shù)與村落有關(guān):
的把握認為絕對貧困戶數(shù)與村落有關(guān):
甲村 | 乙村 | 總計 | |
絕對貧困戶 | |||
相對貧困戶 | |||
總計 |
(2)某干部決定在這兩村貧困指標處于![]() 的貧困戶中,隨機選取
的貧困戶中,隨機選取![]() 戶進行幫扶,用
戶進行幫扶,用![]() 表示所選
表示所選![]() 戶中“亟待幫助戶”的戶數(shù),求
戶中“亟待幫助戶”的戶數(shù),求![]() 的分布列和數(shù)學期望
的分布列和數(shù)學期望![]() .
.
附: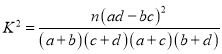 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】以下有關(guān)命題的說法錯誤的是( )
A.命題“若![]() ,則
,則![]() ”的逆否命題為“若
”的逆否命題為“若![]() ,則
,則![]() ”
”
B.“![]() ”是“
”是“![]() ”成立的必要不充分條件
”成立的必要不充分條件
C.對于命題![]() ,使得
,使得![]() ,則
,則![]() ,均有
,均有![]()
D.若![]() 為真命題,則
為真命題,則![]() 與
與![]() 至少有一個為真命題
至少有一個為真命題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
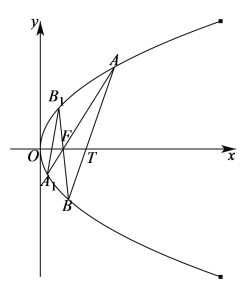
【題目】如圖,拋物線![]() 的焦點為
的焦點為![]() ,過點
,過點![]() 的直線與拋物線
的直線與拋物線![]() 交于點
交于點![]() 、
、![]() ,直線
,直線![]() 、
、![]() 分別與拋物線
分別與拋物線![]() 交于點
交于點![]() 、
、![]() .
.
(1)求拋物線![]() 的標準方程;
的標準方程;
(2)求![]() 與
與![]() 的面積之和的最小值.
的面積之和的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若1路、2路公交車均途經(jīng)泉港一中校門口,其中1路公交車每10分鐘一趟,2路公交車每20分鐘一趟,某生去坐這2趟公交車回家,則等車不超過5分鐘的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2019年春節(jié)期間,某超市準備舉辦一次有獎促銷活動,若顧客一次消費達到400元則可參加一次抽獎活動,超市設(shè)計了兩種抽獎方案.
方案一:一個不透明的盒子中裝有30個質(zhì)地均勻且大小相同的小球,其中10個紅球,20個白球,攪拌均勻后,顧客從中隨機抽取一個球,若抽到紅球則顧客獲得60元的返金券,若抽到白球則獲得20元的返金券,且顧客有放回地抽取3次.
方案二:一個不透明的盒子中裝有30個質(zhì)地均勻且大小相同的小球,其中10個紅球,20個白球,攪拌均勻后,顧客從中隨機抽取一個球,若抽到紅球則顧客獲得80元的返金券,若抽到白球則未中獎,且顧客有放回地抽取3次.
(1)現(xiàn)有兩位顧客均獲得抽獎機會,且都按方案一抽獎,試求這兩位顧客均獲得180元返金券的概率;
(2)若某顧客獲得抽獎機會.
①試分別計算他選擇兩種抽獎方案最終獲得返金券的數(shù)學期望;
②為了吸引顧客消費,讓顧客獲得更多金額的返金券,該超市應(yīng)選擇哪一種抽獎方案進行促銷活動?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在矩形![]() 中,點
中,點![]() 為邊
為邊![]() 上的點,點
上的點,點![]() 為邊
為邊![]() 的中點,
的中點,![]() ,現(xiàn)將
,現(xiàn)將![]() 沿
沿![]() 邊折至
邊折至![]() 位置,且平面
位置,且平面![]() 平面
平面![]() .
.

(1) 求證:平面![]() 平面
平面![]() ;
;
(2) 求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】關(guān)于漸近線方程為![]() 的雙曲線有下述四個結(jié)論:①實軸長與虛軸長相等,②離心率是
的雙曲線有下述四個結(jié)論:①實軸長與虛軸長相等,②離心率是![]() ③過焦點且與實軸垂直的直線被雙曲線截得的線段長與實軸長相等,④頂點到漸近線與焦點到漸近線的距離比值為
③過焦點且與實軸垂直的直線被雙曲線截得的線段長與實軸長相等,④頂點到漸近線與焦點到漸近線的距離比值為![]() .其中所有正確結(jié)論的編號( )
.其中所有正確結(jié)論的編號( )
A.①②B.①③C.①②③D.②③④
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com