
【題目】在某校舉行的航天知識競賽中,參與競賽文科生與理科生人數(shù)之比為![]() ,且成績分布在
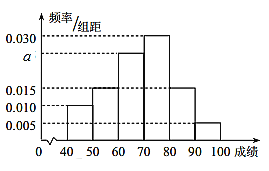
,且成績分布在![]() ,分?jǐn)?shù)在80以上(含80)的同學(xué)獲獎.按文理科用分層抽樣的方法抽取200人的成績作為樣本,得到成績的頻率分布直方圖如圖所示.
,分?jǐn)?shù)在80以上(含80)的同學(xué)獲獎.按文理科用分層抽樣的方法抽取200人的成績作為樣本,得到成績的頻率分布直方圖如圖所示.
文科生 | 理科生 | 合計 | |
獲獎 | 5 | ||
不獲獎 | |||
合計 | 200 |
參考公式: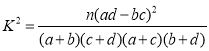 (其中
(其中![]() 為樣本容量)
為樣本容量)
隨機(jī)變量![]() 的概率分布:
的概率分布:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 | |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)求![]() 的值;
的值;
(2)填寫上方的![]() 列聯(lián)表,并判斷能否有超過
列聯(lián)表,并判斷能否有超過![]() 的把握認(rèn)為“獲獎與學(xué)生的文、理科有關(guān)”?
的把握認(rèn)為“獲獎與學(xué)生的文、理科有關(guān)”?
【答案】(1)0.025;(2)聯(lián)表詳見解析,有超過![]() 的把握認(rèn)為“獲獎與學(xué)生的文理科有關(guān)”.
的把握認(rèn)為“獲獎與學(xué)生的文理科有關(guān)”.
【解析】
(1)利用小矩形面積之和為1即可求解![]() 的值.
的值.
(2)由分層抽樣抽取200人,結(jié)合頻率分布直方圖可得獲獎人數(shù)為![]() ,進(jìn)而可得列聯(lián)表,再根據(jù)列聯(lián)表求出觀測值,利用獨立性檢驗的基本思想即可求解.
,進(jìn)而可得列聯(lián)表,再根據(jù)列聯(lián)表求出觀測值,利用獨立性檢驗的基本思想即可求解.
解:(1)由頻率和為1可得![]()
(2)根據(jù)分層抽樣抽取200人,
結(jié)合頻率分布直方圖可得獲獎人數(shù)為![]() ,
,
參與競賽文科生與理科生人數(shù)之比為![]() ,
,
所以競賽文科生為![]() ,
,
列聯(lián)表如下:
文科生 | 理科生 | 合計 | |
獲獎 | 5 | 35 | 40 |
不獲獎 | 45 | 115 | 160 |
合計 | 50 | 150 | 200 |
![]() ,
,
所以有超過![]() 的把握認(rèn)為“獲獎與學(xué)生的文理科有關(guān)”.
的把握認(rèn)為“獲獎與學(xué)生的文理科有關(guān)”.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若對任意![]() ,都有
,都有![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義在R上的函數(shù)f(x)滿足![]() ,
,![]() .
.
(1)求函數(shù)f(x)的解析式;
(2)求函數(shù)g(x)的單調(diào)區(qū)間;
(3)給出定義:若s,t,r滿足![]() ,則稱s比t更接近于r,當(dāng)x≥1時,試比較
,則稱s比t更接近于r,當(dāng)x≥1時,試比較![]() 和
和![]() 哪個更接近
哪個更接近![]() ,并說明理由.
,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]() ,
,![]() .
.
(1)證明:不論![]() 取任何實數(shù),直線
取任何實數(shù),直線![]() 與圓
與圓![]() 恒交于兩點;
恒交于兩點;
(2)當(dāng)直線![]() 被圓
被圓![]() 截得的弦長最短時,求此最短弦長及直線
截得的弦長最短時,求此最短弦長及直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】中國古代十進(jìn)制的算籌計數(shù)法,在數(shù)學(xué)史上是一個偉大的創(chuàng)造.根據(jù)史書的記載和考古材料的發(fā)現(xiàn),古代的算籌實際上是一根根同樣長短和粗細(xì)的小棍子,一般長為![]() ,徑粗
,徑粗![]() ,多用竹子制成,也有用木頭、獸骨、象牙、金屬等材料制成的,大約二百七十幾枚為一束,放在一個布袋里,系在腰部隨身攜帶.需要記數(shù)和計算的時候,就把它們?nèi)〕鰜恚旁谧郎稀⒖簧匣虻厣隙寄軘[弄.在算籌計數(shù)法中,以縱橫兩種排列方式來表示數(shù)字.如圖,是利用算籌表示數(shù)1~9的一種方法.例如:3可表示為“
,多用竹子制成,也有用木頭、獸骨、象牙、金屬等材料制成的,大約二百七十幾枚為一束,放在一個布袋里,系在腰部隨身攜帶.需要記數(shù)和計算的時候,就把它們?nèi)〕鰜恚旁谧郎稀⒖簧匣虻厣隙寄軘[弄.在算籌計數(shù)法中,以縱橫兩種排列方式來表示數(shù)字.如圖,是利用算籌表示數(shù)1~9的一種方法.例如:3可表示為“![]() ”,26可表示為“
”,26可表示為“![]() ”,現(xiàn)有6根算籌,據(jù)此表示方法,若算籌不能剩余,則用這6根算籌能表示的兩位數(shù)的個數(shù)為( )
”,現(xiàn)有6根算籌,據(jù)此表示方法,若算籌不能剩余,則用這6根算籌能表示的兩位數(shù)的個數(shù)為( )
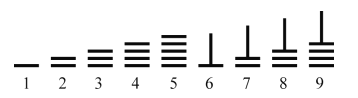
A.13B.14C.15D.16
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù) ,
,![]() ,
,![]() 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(1)若![]() ,
,![]() ,證明:當(dāng)
,證明:當(dāng)![]() 時,
時,![]() 恒成立;
恒成立;
(2)若![]() ,
,![]() ,
,![]() 在
在![]() 上存在兩個極值點,求
上存在兩個極值點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】二次函數(shù)![]() 圖像與
圖像與![]() 軸交于
軸交于![]() ,
,![]() 兩點,交直線
兩點,交直線![]() 于
于![]() ,
,![]() 兩點,經(jīng)過三點
兩點,經(jīng)過三點![]() ,
,![]() ,
,![]() 作圓
作圓![]() .
.
(1)求證:當(dāng)![]() 變化時,圓
變化時,圓![]() 的圓心在一條定直線上;
的圓心在一條定直線上;
(2)求證:圓![]() 經(jīng)過除原點外的一個定點.
經(jīng)過除原點外的一個定點.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2018年9月24日,阿貝爾獎和菲爾茲獎雙料得主、英國著名數(shù)學(xué)家阿蒂亞爵士宣布自己證明了黎曼猜想,這一事件引起了數(shù)學(xué)屆的震動。在1859年的時候,德國數(shù)學(xué)家黎曼向科學(xué)院提交了題目為《論小于某值的素數(shù)個數(shù)》的論文并提出了一個命題,也就是著名的黎曼猜想。在此之前,著名數(shù)學(xué)家歐拉也曾研究過這個問題,并得到小于數(shù)字![]() 的素數(shù)個數(shù)大約可以表示為
的素數(shù)個數(shù)大約可以表示為![]() 的結(jié)論。若根據(jù)歐拉得出的結(jié)論,估計1000以內(nèi)的素數(shù)的個數(shù)為_________(素數(shù)即質(zhì)數(shù),
的結(jié)論。若根據(jù)歐拉得出的結(jié)論,估計1000以內(nèi)的素數(shù)的個數(shù)為_________(素數(shù)即質(zhì)數(shù),![]() ,計算結(jié)果取整數(shù))
,計算結(jié)果取整數(shù))
A. 768 B. 144 C. 767 D. 145
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com