
某地區對12歲兒童瞬時記憶能力進行調查.瞬時記憶能力包括聽覺記憶能力與視覺記憶能力.某班學甲、乙兩人參加一次英語口語考試,已知在備選的10道試題中,甲能答對其中的6題,乙能答對其中的8題.規定每次考試都從備選題中隨機抽出3題進行測試,至少答對2題才算合格.(1)求甲、乙兩人考試均合格的概率;(2)求甲答對試題數 的概率分布及數學期望.
的概率分布及數學期望.
(1) ;
;
(2)ξ 0 1 2 3 P 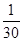
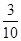
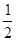
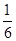
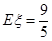
解析試題分析:(1)每人參加考試合格,必須且只需從備選的10個題中隨機抽出3題進行測試,至少答對2題才算合格,即恰好答對2題或恰好答對3題,由已知及古典型概率公式可求出甲、乙兩人考試分別合格的概率,且知兩人參加考試合格的事件是相互獨立的,從而由相互獨立事件同時發生的概率積公式可求得甲、乙兩人考試均合格的概率;(2)由于每次考試都從備選題中隨機抽出3題進行測試,故甲答對試題數 的所有可能取值只可能是:0,1,2,3.不可能再有第四種可能了,應用古典型概率計算公式,可計算出
的所有可能取值只可能是:0,1,2,3.不可能再有第四種可能了,應用古典型概率計算公式,可計算出 的每一個取值對應事件的概率,從而得到甲答對試題數ξ的概率分布及數學期望.
的每一個取值對應事件的概率,從而得到甲答對試題數ξ的概率分布及數學期望.
試題解析:(1)設甲、乙兩人考試合格的事件分別為A、B,則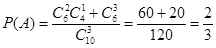 ,
,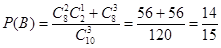 ;因為事件A、B相互獨立,所以甲、乙兩人考試均合格的概率為:
;因為事件A、B相互獨立,所以甲、乙兩人考試均合格的概率為: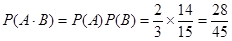 .答:甲、乙兩人考試均合格的概率為
.答:甲、乙兩人考試均合格的概率為 .
.
(2)依題意,知 的所有可能取值為:0,1,2,3.則
的所有可能取值為:0,1,2,3.則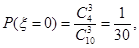
 ,
,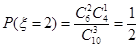 ,
,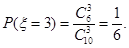
甲答對試題數ξ的概率分布如下:ξ 0 1 2 3 P 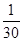
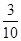
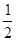
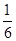
甲答對試題數ξ的數學期望 12分
12分
考點:1.古典概率;2.隨機變量的分布列;3.數學期望.


科目:高中數學 來源: 題型:解答題
在一個盒子中,放有標號分別為1,2,3的三張卡片,現從這個盒子中,有放回地先后抽得兩張卡片的標號分別為x、y,記ξ=|x-2|+|y-x|.
(1)求隨機變量ξ的最大值,并求事件“ξ取得最大值”的概率;
(2)求隨機變量ξ的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一個均勻的正方體玩具,各個面上分別寫有1,2,3,4,5,6,將這個玩具先后拋擲2次,求:
(1)朝上的一面數相等的概率;(2)朝上的一面數之和小于5的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知方程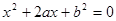 是關于
是關于 的一元二次方程.
的一元二次方程.
(1)若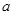 是從集合
是從集合 四個數中任取的一個數,
四個數中任取的一個數,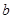 是從集合
是從集合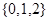 三個數中任取的一個數,求上述方程有實數根的概率;
三個數中任取的一個數,求上述方程有實數根的概率;
(2)若 ,
, ,求上述方程有實數根的概率.
,求上述方程有實數根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(12分)將一顆骰子先后拋擲2次,觀察向上的點數,求:
(1)兩數之和為6的概率;
(2)兩數之積是6的倍數的概率;
(3)以第一次向上點數為橫坐標x,第二次向上的點數為縱坐標y的點(x,y)在圓x2+y2=15的內部的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)把一顆質地均勻,四個面上分別標有復數 ,
,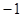 ,
,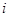 ,
,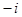 (
(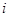 為虛數單位)的正四面體玩具連續拋擲兩次,第一次出現底面朝下的復數記為
為虛數單位)的正四面體玩具連續拋擲兩次,第一次出現底面朝下的復數記為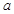 ,第二次出現底面朝下的復數記為
,第二次出現底面朝下的復數記為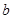 .
.
(1)用 表示“
表示“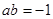 ”這一事件,求事件
”這一事件,求事件 的概率
的概率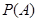 ;
;
(2)設復數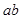 的實部為
的實部為 ,求
,求 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了解某班關注NBA(美國職業籃球)是否與性別有關,對某班48人進行了問卷調查得到如下的列聯表:
| | 關注NBA | 不關注NBA | 合計 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合計 | | | 48 |
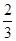 .
.| P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com