
【題目】在四棱錐P﹣ABCD中,底面ABCD為直角梯形,∠BAD=∠ADC=90°,DC=2AB=2AD,BC⊥PD,E,F分別是PB,BC的中點. 
求證:
(1)PC∥平面DEF;
(2)平面PBC⊥平面PBD.
【答案】
(1)證明:∵E,F分別是PB,BC的中點,
∴PC∥EF,
又PC平面DEF,EF平面DEF,
∴PC∥平面DEF
(2)證明:取CD的中點M,連結BM,
則AB ![]() DM,又AD⊥AB,AB=AD,
DM,又AD⊥AB,AB=AD,
∴四邊形ABMD是正方形,
∴BM⊥CD,BM=CM=DM=1,BD= ![]() ,
,
∴BC= ![]() ,
,
∴BD2+BC2=CD2,
∴BC⊥BD,又BC⊥PD,BD∩PD=D,
∴BC⊥平面PBD,
又BC平面PBC,
∴平面PBC⊥平面PBD.

【解析】(1)由中位線定理可得PC∥EF,故而PC∥平面DEF;(2)由直角梯形可得BC⊥BD,結合BC⊥PD得出BC⊥平面PBD,于是平面PBC⊥平面PBD.
【考點精析】解答此題的關鍵在于理解直線與平面平行的判定的相關知識,掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行,以及對平面與平面垂直的判定的理解,了解一個平面過另一個平面的垂線,則這兩個平面垂直.


科目:高中數學 來源: 題型:
【題目】最新公布的《道路交通安全法》和《道路交通安全法實施條例》對車速、安全車距以及影響駕駛人反應快慢等因素均有詳細規定,這些規定說到底主要與剎車距離有關,剎車距離是指從駕駛員發現障礙到制動車輛,最后完全停止所行駛的距離,即:剎車距離=反應距離+制動距離,反應距離=反應時間×速率,制動距離與速率的平方成正比,某反應時間為![]() 的駕駛員以
的駕駛員以![]() 的速率行駛,遇緊急情況,汽車的剎車距離為
的速率行駛,遇緊急情況,汽車的剎車距離為![]() .
.
(![]() )試將剎車距離
)試將剎車距離![]() 表示為速率
表示為速率![]() 的函數.
的函數.
(![]() )若該駕駛員駕駛汽車在限速為
)若該駕駛員駕駛汽車在限速為![]() 的公路上行駛,遇緊急情況,汽車的剎車距離為
的公路上行駛,遇緊急情況,汽車的剎車距離為![]() ,試問該車是否超速?請說明理由.
,試問該車是否超速?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某加油站20名員工日銷售量的頻率分布直方圖,如圖所示:
(1)補全該頻率分布直方圖在[20,30)的部分,并分別計算日銷售量在 [10,20),[20,30)的員工數;
(2)在日銷量為[10,30)的員工中隨機抽取2人,求這兩名員工日銷量在 [20,30)的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數列{an}中,an=cos ![]() (n∈N*)
(n∈N*)
(1)試將an+1表示為an的函數關系式;
(2)若數列{bn}滿足bn=1﹣ ![]() (n∈N*),猜想an與bn的大小關系,并證明你的結論.
(n∈N*),猜想an與bn的大小關系,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,橢圓 ![]() +
+ ![]() =1(a>b>0)的離心率為e,D為右準線上一點.
=1(a>b>0)的離心率為e,D為右準線上一點.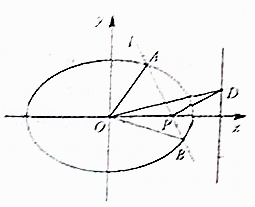
(1)若e= ![]() ,點D的橫坐標為4,求橢圓的方程;
,點D的橫坐標為4,求橢圓的方程;
(2)設斜率存在的直線l經過點P( ![]() ,0),且與橢圓交于A,B兩點.若
,0),且與橢圓交于A,B兩點.若 ![]() +
+ ![]() =
= ![]() ,DP⊥l,求橢圓離心率e.
,DP⊥l,求橢圓離心率e.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】公元263年左右,我國古代數學家劉徽用圓內接正多邊形的面積去逼近圓的面積求圓周率π,劉徽稱這個方法為“割圓術”,并且把“割圓術”的特點概括為“割之彌細,所失彌少,割之又割,以至于不可割,則與圓周合體而無所失矣”下圖是根據劉徽的“割圓術”思想設計的一個程序框圖.若運行該程序,則輸出的n的值為:(參考數據: ![]() ≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)( )
≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)( ) 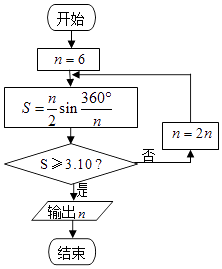
A.48
B.36
C.30
D.24
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在D上的函數 ![]() ,若滿足:
,若滿足: ![]() ,都有
,都有 ![]() 成立,則稱
成立,則稱 ![]() 是D上的有界函數,其中M稱為函數
是D上的有界函數,其中M稱為函數 ![]() 的上界.
的上界.
(I)設 ![]() ,證明:
,證明: ![]() 在
在 ![]() 上是有界函數,并寫出
上是有界函數,并寫出 ![]() 所有上界的值的集合;
所有上界的值的集合;
(II)若函數 ![]() 在
在 ![]() 上是以3為上界的有界函數,求實數a的取值范圍.
上是以3為上界的有界函數,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com