
某地區有小學21所,中學14所,大學7所,現采取分層抽樣的方法從這些學校中抽取6所學校對學生進行視力調查。
(1)求應從小學、中學、大學中分別抽取的學校數目;
(2)若從抽取的6所學校中隨機抽取2所學校,求抽取的2所學校均為小學的概率.
(1)從小學、中學、大學中分別抽取的學校數目為3、2、1;
(2)抽取的2所學校均為小學的概率為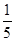 .
.
解析試題分析:(1)由分層抽樣易求從小學、中學、大學中分別抽取的學校數目為3、2、1;
(2)先列舉出從抽取的6所學校中隨機抽取2所學校的所有可能,找出抽取的2所學校均為小學可能,即可求出抽取的2所學校均為小學的概率.
試題解析:(1)從小學、中學、大學中分別抽取的學校數目之比為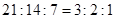 ,得:從小學、中學、大學中分別抽取的學校數目為
,得:從小學、中學、大學中分別抽取的學校數目為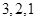 .
.
(2)設抽取的6所學校中小學為 ,中學位
,中學位 ,大學為
,大學為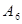 ;抽取2所學校的結果為:
;抽取2所學校的結果為: 
 共15種;抽取的2所學校均為小學的結果為
共15種;抽取的2所學校均為小學的結果為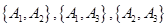 共3種,抽取的2所學校均為小學的概率為
共3種,抽取的2所學校均為小學的概率為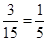 .
.
考點:分層抽樣、古典概型.


科目:高中數學 來源: 題型:解答題
已知 、
、 兩個盒子中分別裝有標記為
兩個盒子中分別裝有標記為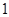 ,
, ,
, ,
, 的大小相同的四個小球,甲從
的大小相同的四個小球,甲從 盒中等可能地取出
盒中等可能地取出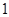 個球,乙從
個球,乙從 盒中等可能地取出
盒中等可能地取出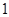 個球.
個球.
(1)用有序數對 表示事件“甲抽到標號為
表示事件“甲抽到標號為 的小球,乙抽到標號為
的小球,乙抽到標號為 的小球”,試寫出所有可能的事件;
的小球”,試寫出所有可能的事件;
(2)甲、乙兩人玩游戲,約定規則:若甲抽到的小球的標號比乙大,則甲勝;反之,則乙勝.你認為此規則是否公平?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲乙兩個同學進行定點投籃游戲,已知他們每一次投籃投中的概率均為 ,且各次投籃的結果互不影響.甲同學決定投5次,乙同學決定投中1次就停止,否則就繼續投下去,但投籃次數不超過5次.
,且各次投籃的結果互不影響.甲同學決定投5次,乙同學決定投中1次就停止,否則就繼續投下去,但投籃次數不超過5次.
(1)求甲同學至少有4次投中的概率;
(2)求乙同學投籃次數 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某產品的三個質量指標分別為x,y,z,用綜合指標S=x+y+z評價該產品的等級.若S≤4,則該產品為一等品.先從一批該產品中,隨機抽取10件產品作為樣本,其質量指標列表如下:
| 產品編號 | A1 | A2 | A3 | A4 | A5 |
| 質量指標(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| 產品編號 | A6 | A7 | A8 | A9 | A10 |
| 質量指標(x,y,z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
從1,2,3,4,5,6中不放回地隨機抽取四個數字,記取得的四個數字之和除以4的余數為 ,除以3的余數為
,除以3的余數為
(1)求X=2的概率;
(2)記事件 為事件
為事件 ,事件
,事件 為事件
為事件 ,判斷事件
,判斷事件 與事件
與事件 是否相互獨立,并給出證明.
是否相互獨立,并給出證明.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數y=x-1,令x=―4,―3,―2,-1,0,1,2,3,4,可得函數圖象上的九個點,在這九個點中隨機取出兩個點P1(x1,y1),P2(x2,y2),
(1)求P1,P2兩點在雙曲線xy=6上的概率;
(2)求P1,P2兩點不在同一雙曲線xy=k(k≠0)上的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙兩運動員進行射擊訓練,已知他們擊中目標的環數都穩定在7,8,9,10環,且每次射擊成績互不影響,射擊環數的頻率分布表如下:
甲運動員
| 射擊環數 | 頻數 | 頻率 |
| 7 | 10 | 0.1 |
| 8 | 10 | 0.1 |
| 9 | x | 0.45 |
| 10 | 35 | y |
| 合計 | 100 | 1 |
| 射擊環數 | 頻數 | 頻率 |
| 7 | 8 | 0.1 |
| 8 | 12 | 0.15 |
| 9 | z | |
| 10 | | 0.35 |
| 合計 | 80 | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
近幾年來,我國許多地區經常出現干旱現象,為抗旱經常要進行人工降雨.現由天氣預報得知,某地在未來5天的指定時間的降雨概率是:前3天均為50%,后2天均為80%,5天內任何一天的該指定時間沒有降雨,則在當天實行人工降雨,否則,當天不實施人工降雨.
(1)求至少有1天需要人工降雨的概率.
(2)求不需要人工降雨的天數x的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設ξ為隨機變量,從棱長為1的正方體的12條棱中任取兩條,當兩條棱相交時,ξ=0;當兩條棱平行時,ξ的值為兩條棱之間的距離;當兩條棱異面時,ξ=1.
(1)求概率P(ξ=0);
(2)求ξ的分布列,并求其數學期望E(ξ).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com