
如圖所示,質點P在正方形ABCD的四個頂點上按逆時針方向前進.現在投擲一個質地均勻、每個面上標有一個數字的正方體玩具,它的六個面上分別寫有兩個1、兩個2、兩個3一共六個數字.質點P從A點出發,規則如下:當正方體上底面出現的數字是1,質點P前進一步(如由A到B);當正方體上底面出現的數字是2,質點P前進兩步(如由A到C),當正方體上底面出現的數字是3,質點P前進三步(如由A到D).在質點P轉一圈之前連續投擲,若超過一圈,則投擲終止.

(1)求質點P恰好返回到A點的概率;
(2)在質點P轉一圈恰能返回到A點的所有結果中,用隨機變量ξ表示點P恰能返回到A點的投擲次數,求ξ的數學期望.
(1)質點P恰好返回到A點的概率為:P=P2+P3+P4=37/81.
(2)Eξ=19/7.
【解析】本試題主要是考查了古典概型概率的計算公式,以及利用獨立事件的概率的乘法公式得到概率值,并且得到隨機變量各個取值的概率值,從而得到分布列和期望值。
(1)先分析實驗中所有的基本事件,然后利用等可能時間的概率公式得到結論。同時要結合獨立試驗的概率公式表示得到。
(2)利用第一問中的結論,可知ξ的可能取值為2,3,4,然后分別得到各自的概率值,求解得到。
解析:(1)投擲一次正方體玩具,每個數字在上底面出現都是等可能的,其概率為P1==.
只投擲一次不可能返回到A點;若投擲兩次質點P就恰好能返回到A點,則上底面出現的兩個數字應依次為:(1,3)、(3,1)、(2,2)三種結果,其概率為P2=()2×3=;
若投擲三次質點P恰能返回到A點,則上底面出現的三個數字應依次為:(1,1,2)、(1,2,1)、(2,1,1)三種結果,其概率為P3=()3×3=;
若投擲四次質點P恰能返回到A點,則上底面出現的四個數字應依次為:(1,1,1,1).其概率為P4=()4=.
所以,質點P恰好返回到A點的概率為:P=P2+P3+P4=++=. 6分
(2)由(1)知,質點P轉一圈恰能返回到A點的所有結果共有以上問題中的7種情況,且ξ的可能取值為2,3,4,
則P(ξ=2)=,P(ξ=3)=,P(ξ=4)=,
所以,Eξ=2×+3×+4×=.


 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:高中數學 來源: 題型:
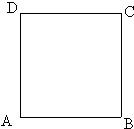 如圖所示,質點P在正方形ABCD的四個頂點上按逆時針方向前進.現在投擲一個質地均勻.每個面上標有一個數字的正方體玩具,它的六個面上分別寫有兩個1.兩個2.兩個3一共六個數字.質點P從A點出發,規則如下:當正方體上底面出現的數字是1,質點P前進一步(如由A到B);當正方體上底面出現的數字是2,質點P前進兩步(如由A到C),當正方體上底面出現的數字是3,質點P前進三步(如由A到D).在質點P轉一圈之前連續投擲,若超過一圈,則投擲終止.
如圖所示,質點P在正方形ABCD的四個頂點上按逆時針方向前進.現在投擲一個質地均勻.每個面上標有一個數字的正方體玩具,它的六個面上分別寫有兩個1.兩個2.兩個3一共六個數字.質點P從A點出發,規則如下:當正方體上底面出現的數字是1,質點P前進一步(如由A到B);當正方體上底面出現的數字是2,質點P前進兩步(如由A到C),當正方體上底面出現的數字是3,質點P前進三步(如由A到D).在質點P轉一圈之前連續投擲,若超過一圈,則投擲終止.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖所示,質點P在正方形ABCD的四個頂點上按逆時針方向前進.現在投擲一個質地均勻、每個面上標有一個數字的正方體玩具,它的六個面上分別寫有兩個1、兩個2、兩個3一共六個數字.質點P從A點出發,規則如下:當正方體上底面出現的數字是1,質點P前進一步(如由A到B);當正方體上底面出現的數字是2,質點P前進兩步(如由A到C);當正方體上底面出現的數字是3,質點P前進三步(如由A到D).在質點P轉一圈之前連續投擲,若超過一圈,則投擲終止.
如圖所示,質點P在正方形ABCD的四個頂點上按逆時針方向前進.現在投擲一個質地均勻、每個面上標有一個數字的正方體玩具,它的六個面上分別寫有兩個1、兩個2、兩個3一共六個數字.質點P從A點出發,規則如下:當正方體上底面出現的數字是1,質點P前進一步(如由A到B);當正方體上底面出現的數字是2,質點P前進兩步(如由A到C);當正方體上底面出現的數字是3,質點P前進三步(如由A到D).在質點P轉一圈之前連續投擲,若超過一圈,則投擲終止.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖所示,質點P在正方形ABCD的四個頂點上按逆時針方向前進. 現在投擲一個質地均勻、每個面上標有一個數字的正方體玩具,它的六個面上分別寫有兩個1、兩個2、兩個3一共六個數字. 質點P從A點出發,規則如下:當正方體上底面出現的數字是1,質點P前進一步(如由A到B);當正方體上底面出現的數字是2,質點P前兩步(如由A到C),當正方體上底面出現的數字是3,質點P前進三步(如由A到D). 在質點P轉一圈之前連續投擲,若超過一圈,則投擲終止.
如圖所示,質點P在正方形ABCD的四個頂點上按逆時針方向前進. 現在投擲一個質地均勻、每個面上標有一個數字的正方體玩具,它的六個面上分別寫有兩個1、兩個2、兩個3一共六個數字. 質點P從A點出發,規則如下:當正方體上底面出現的數字是1,質點P前進一步(如由A到B);當正方體上底面出現的數字是2,質點P前兩步(如由A到C),當正方體上底面出現的數字是3,質點P前進三步(如由A到D). 在質點P轉一圈之前連續投擲,若超過一圈,則投擲終止.查看答案和解析>>
科目:高中數學 來源: 題型:
 (本題滿分13分) 如圖所示,質點P在正方形ABCD的四個頂點上按逆時針方向前進.現在投擲一個質地均勻、每個面上標有一個數字的正方體玩具,它的六個面上分別寫有兩個1、兩個2、兩個3一共六個數字.質點P從A點出發,規則如下:當正方體上底面出現的數字是1,質點P前進一步(如由A到B);當正方體上底面出現的數字是2,質點P前進兩步(如由A到C),
(本題滿分13分) 如圖所示,質點P在正方形ABCD的四個頂點上按逆時針方向前進.現在投擲一個質地均勻、每個面上標有一個數字的正方體玩具,它的六個面上分別寫有兩個1、兩個2、兩個3一共六個數字.質點P從A點出發,規則如下:當正方體上底面出現的數字是1,質點P前進一步(如由A到B);當正方體上底面出現的數字是2,質點P前進兩步(如由A到C),
當正方體上底面出現的數字是3,質點P前進三步(如由A到![]() ).
).
在質點P轉一圈之前連續投擲,若超過一圈,則投擲終止.
(Ⅰ)求點P恰好返回到A點的概率;
(Ⅱ)在點P轉一圈恰能返回到A點的所有結果中,
用隨機變量![]() 表示點P恰能返回到A點的投擲次數,求
表示點P恰能返回到A點的投擲次數,求![]() 的數學期望.
的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com