
��С�}�M��12�֣���֪��(sh��)��(sh��) ��
��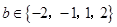 ��
��
�������c(di��n)��a��b���ڵ�һ���ĸ��ʣ�
������ֱ��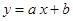 �c�A
�c�A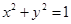 �й����c(di��n)�ĸ��ʣ�
�й����c(di��n)�ĸ��ʣ�
�⣺���ڌ�(sh��)��(sh��)��(du��) ������ȡֵ�飺
������ȡֵ�飺 ��
�� ��
�� ��
�� ��
�� ��
�� ��
�� ��
�� ��
�� ��
�� ��
�� ��
�� ��
�� ��
�� ��
�� ��
�� ����16�N��
����16�N��
�O(sh��)���c(di��n)��a��b���ڵ�һ���ޡ����¼� ����ֱ��
����ֱ�� �c�A
�c�A �й����c(di��n)�����¼�
�й����c(di��n)�����¼� ��
��
��1�����c(di��n)��a��b���ڵ�һ���ޣ��t��횝M��
���M��l����(sh��)��(sh��)��(du��) ��
�� ��
�� ��
�� ��
�� ����4�N��
����4�N��
�� ����ֱ��
����ֱ�� ����(j��ng)�^�������ĸ��ʞ�
����(j��ng)�^�������ĸ��ʞ� ��
��
��2����ֱ�� �c�A
�c�A �й����c(di��n)���t��횝M��
�й����c(di��n)���t��횝M�� ��1����
��1���� ��
�� ��
��
�� ���t
���t ����Ҫ�˕r(sh��)��(sh��)��(sh��)��(du��)��
����Ҫ�˕r(sh��)��(sh��)��(sh��)��(du��)�� ����4�N��ͬȡֵ��
����4�N��ͬȡֵ��
�� ���t
���t ����Ҫ�˕r(sh��)��(sh��)��(sh��)��(du��)��
����Ҫ�˕r(sh��)��(sh��)��(sh��)��(du��)�� ����2�N��ͬȡֵ��
����2�N��ͬȡֵ��
�� ���t
���t ����Ҫ�˕r(sh��)��(sh��)��(sh��)��(du��)��
����Ҫ�˕r(sh��)��(sh��)��(sh��)��(du��)�� ����2�N��ͬȡֵ��
����2�N��ͬȡֵ��
�� ���t
���t ����Ҫ�˕r(sh��)��(sh��)��(sh��)��(du��)��
����Ҫ�˕r(sh��)��(sh��)��(sh��)��(du��)�� ����4�N��ͬȡֵ�����M��l���Č�(sh��)��(sh��)��(du��)
����4�N��ͬȡֵ�����M��l���Č�(sh��)��(sh��)��(du��) ����12�N��ͬȡֵ����
����12�N��ͬȡֵ���� �� ��ֱ��
�� ��ֱ�� �c�A
�c�A �й����c(di��n)�ĸ��ʞ�
�й����c(di��n)�ĸ��ʞ� ��
��
����������ԇ�}��Ҫ�ǿ����˹ŵ�����ʵĹ�ʽ���\(y��n)�á�
��1����?y��n)����ԇ�?y��n)�Ļ����¼����g�ǽ�Q���}�ĵ�һҪ�أ�Ȼ���M(j��n)һ�������¼��l(f��)���Ļ����¼���(sh��)���Y(ji��)�ϸ��ʹ�ʽ�õ���
��2����?y��n)�ֱ�� �c�A
�c�A �й����c(di��n)���t��횝M��
�й����c(di��n)���t��횝M�� ��1����
��1���� ��
�� ��Ȼ������M�㲻���ǵ�a,b�ĽM���ж��٣�Ȼ��õ�����ֵ��
��Ȼ������M�㲻���ǵ�a,b�ĽM���ж��٣�Ȼ��õ�����ֵ��


 ���~���ƪϵ�д�
���~���ƪϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2010-2011�W(xu��)���|��ʡ�|�υf(xi��)���w��һ�W(xu��)�����п�ԇ��(sh��)�W(xu��)������ �}�ͣ�����}
����С�}�M��12�֣�
��֪���� ��ӛ����(sh��)
��ӛ����(sh��) ��
��
������(sh��) ����С�����ڞ�
����С�����ڞ� .
.
��1���� ��ֵ��
��ֵ��
��2����(d��ng) �r(sh��)��ԇ��
�r(sh��)��ԇ�� ��ֵ��
��ֵ��
��3���� ��
�� �ϵĆ��{(di��o)�f���^(q��)�g��
�ϵĆ��{(di��o)�f���^(q��)�g��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2011�ú�����ʡ��c��(sh��)�(y��n)�ЌW(xu��)�����߿�����ģ�Mԇ�}�픵(sh��) �}�ͣ�����}
������С�}�M��12�֣�
��֪�E�A
 �ǙE�A�Ͽv����(bi��o)������ă��c(di��n)����
�ǙE�A�Ͽv����(bi��o)������ă��c(di��n)���� ����F��E�A�����c(di��n)��
����F��E�A�����c(di��n)��
������E�A�ķ��̣�
������AB�Ĵ�ֱƽ�־���y�S�ϵĽؾ��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2011�꽭��ʡ��ͨ����������ԇ�ĿƔ�(sh��)�W(xu��) �}�ͣ�����}
(��С�}�M��12�֣�
��֪�^���タ �Ľ��c(di��n)��б�ʞ�
�Ľ��c(di��n)��б�ʞ� ��ֱ�������タ��
��ֱ�������タ��
 ��
�� �����c(di��n)����
�����c(di��n)���� ��
��
��1����ԓ���タ�ķ��̣�
��2�� ������(bi��o)ԭ�c(di��n)��
������(bi��o)ԭ�c(di��n)�� �钁�タ��һ�c(di��n)����
�钁�タ��һ�c(di��n)���� ����
���� ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2012-2013�W(xu��)������`��������(j��)�ЌW(xu��)�����όW(xu��)�ڵ������|(zh��)���z�y(c��)�Ĕ�(sh��)�W(xu��)ԇ���������棩 �}�ͣ�����}
����С�}�M��12�֣�
��֪�l�� ��
��
�l�� ��
��
��1���� ����(sh��)��(sh��)
����(sh��)��(sh��) ��ֵ;
��ֵ;
(2)�� ,��(sh��)��(sh��)
,��(sh��)��(sh��) ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2012-2013�W(xu��)��ӱ�ʡ���������hһ���R��һ�и���(li��n)�����Ɣ�(sh��)�W(xu��)ԇ���������棩 �}�ͣ�����}
����С�}�M��12�֣�
��֪����(sh��) ���Ҍ�(du��)�����⌍(sh��)��(sh��)
���Ҍ�(du��)�����⌍(sh��)��(sh��) ������
������ ��
��
��1����(sh��) �Ľ���ʽ��
�Ľ���ʽ��
��2������(sh��)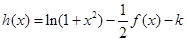 �Ўׂ�(g��)���c(di��n)��
�Ўׂ�(g��)���c(di��n)��
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com