
已知函數f(x)=ax2+bx+c,其中a∈N*,b∈N,c∈Z。
(1)若b>2a,且f(sinx)(x∈R)的最大值為2,最小值為-4,試求函數f(x)的最小值;
(2)若對任意實數x,不等式4x≤f(x)≤2(x2+1)恒成立,且存在x0,使得f(x0)<2(x02+1)成立,求c的值。
(1)f(x)=x2+3x-2,最小值為-17/4。
(2)c=1。
(1)由函數f(x)的圖像開口向上,對稱軸x=-b/2a<-1知,f(x)在[-1,1]上為增函數,故f(1)=a+b+c=2,f(-1)=a-b+c=-4,∴b=3,a+c=-1。又b>2a,故a=1,c=-2。∴f(x)=x2+3x-2,最小值為-17/4。
(2)令x=1,代入不等式4x≤f(x)≤2(x2+1)得f(1)=4,即a+b+c=4,從而b=4-a-c。又4x≤f(x)恒成立,得ax2+(b-4)x+c≥0恒成立,故△=(b-4)2-4ac≤0,∴a=c。又b≥0,a+c≤4,∴c=1或c=2。當c=2時,f(x)=2x2+2,此時不存在滿足題意的x0。當c=1時滿足條件,故c=1。


科目:高中數學 來源:數學教研室 題型:044
(1)求函數f(x)的解析式;
(2)記![]() (n),n是正整數,
(n),n是正整數,![]() 是數列{
是數列{![]() }的前n項和,解關于n的不等式
}的前n項和,解關于n的不等式![]() ;
;
(3)對于(2)中的![]() 與
與![]() ,整數
,整數![]() 是否為數列{
是否為數列{![]() }中的項?若是,則求出相應的項數;若不是,則說明理由.
}中的項?若是,則求出相應的項數;若不是,則說明理由.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年河南省五市高三第二次聯考理科數學 題型:解答題
(本小題滿分12分)
已知函數f(x)= -x (e為自然對數的底數).
-x (e為自然對數的底數).
(Ⅰ)求f(x)的最小值;
(Ⅱ)不等式f(x)>ax的解集為P,若M={x| ≤x≤2}且M∩P≠
≤x≤2}且M∩P≠ ,求實數a的
,求實數a的
取值范圍;
(Ⅲ)已知n∈N﹡,且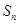 =
= (t為常數,t≥0),是否存在等比數列{
(t為常數,t≥0),是否存在等比數列{ },使得b1+b2+…
},使得b1+b2+… =
=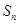 ?若存在,請求出數列{
?若存在,請求出數列{ }的通項公式;若不存在,請說明理由.
}的通項公式;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2012屆遼寧省大連市高二上學期期末考試(文科)試題 題型:解答題
已知函數f(x)=x3+ax2+bx+1在x=- 與x=1時都取得極值。
與x=1時都取得極值。
(1)求a、b的值與函數f(x)的單調區間;
(2)求函數f(x)的單調區間
查看答案和解析>>
科目:高中數學 來源: 題型:
(1)求函數f(x)的解析式;
(2)記an=log2f(n),n是正整數,Sn是數列{an}的前n項和,解關于n的不等式anSn≤0;
(3)對于(2)中的an與Sn,整數104是否為數列{anSn}中的項?若是,則求出相應的項數;若不是,則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
(1)求函數f(x)的解析式;
(2)記an=log2f(n),n是正整數,Sn是數列{an}的前n項和,解關于n的不等式anSn≤0;
(3)對于(2)中的an與Sn,整數964是否為數列{anSn}中的項?若是,則求出相應的項數;若不是,則說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com