

| A. | (-∞,0) | B. | (4,+∞) | C. | (-∞,2) | D. | (2,+∞) |
科目:高中數學 來源: 題型:選擇題
| A. | {0,1,2,3,4} | B. | {0,1} | C. | {0,1,4} | D. | {1,2} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
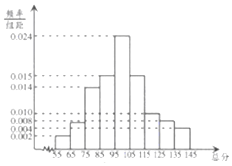 從某市統考的學生數學考試卷中隨機抽查100份數學試卷作為樣本,分別統計出這些試卷總分,由總分得到如下的頻率分布直方圖.
從某市統考的學生數學考試卷中隨機抽查100份數學試卷作為樣本,分別統計出這些試卷總分,由總分得到如下的頻率分布直方圖.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 如果平面α⊥平面 γ,平面β⊥平面 γ,α∩β=l,那么l⊥γ | |
| B. | 如果平面α⊥平面 β,那么平面α內一定存在直線平行于平面β | |
| C. | 如果平面α不垂直于平面β,那么平面α內一定不存在直線垂直于平面β | |
| D. | 如果平面α⊥平面 β,過α內任意一點作交線的垂線,那么此垂線必垂直于β |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
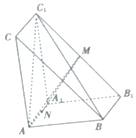 如圖,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分別為B1C1,AA1的中點
如圖,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分別為B1C1,AA1的中點查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com