日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
已知向量
h
=(cosB，cosA)，
k
=(sinA，-sinB)，
h
•
k
=
3
5
sinC，其中A、B、C分別是△ABC的三內角．
（1）求
tanA
tanB
的值；
（2）求tan（A-B）的最大值．
分析：（1）由數量積和三角函數公式可得sinAcosB=4sinBcosA，由同角三角函數的基本關系可得
tanA
tanB
=4；（2）由（1）知：tanA=4tanB，必有tanB＞0，又可得tan（A+B）=
3
4tanB+
1
tanB
，由基本不等式的知識可得．
解答：解：（1）由
h
•
k
=
3
5
sinC可得sinAcosB-sinBcosA=
3
5
sinC
又∵A+B+C=π，sinC=sin（A+B），
化簡得：sinAcosB=4sinBcosA，變形得
tanA
tanB
=4
（2）由（1）知：tanA=4tanB，必有tanB＞0，
否則若tanB＜0，則tanA＜0，角AB均為鈍角，與三角形的內角矛盾，
∴tan(A-B)=
tanA-tanB
1+tanAtanB
=
3tanB
1+4tan2B
=
3
4tanB+
1
tanB

由基本不等式可得
3
4tanB+
1
tanB
≤
3
2
4tanB•
1
tanB
=
3
4

當且僅當4tanB=
1
4tanB
，即tanB=
1
2
時，tan（A+B）=
3
4tanB+
1
tanB
取最大值
3
4
點評：本題考查數量積與三角函數的知識，涉及兩角和與差的正切函數以及基本不等式，屬中檔題．
練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

已知函數f(x)=2sin(x+
π
6
)-2cosx．
（1）當x∈[
π
2
，π]時，若sinx=
4
5
，求函數f（x）的值；
（2）當x∈[
π
2
，π]時，求函數h(x)=3sin(
π
6
-x)-cos(2x-
π
3
)的值域；
（3）把函數y=f（x）的圖象按向量
m
平移得到函數g（x）的圖象，若函數g（x）是偶函數，寫出|
m
|最小的向量
m
的坐標．

查看答案和解析>>

科目：高中數學 來源： 題型：

定義非零向量
OM
=(a，b)的“相伴函數”為f（x）=asinx+bcosx（x∈R），向量
OM
=(a，b)稱為函數f（x）=asinx+bcosx的“相伴向量”（其中O為坐標原點）．記平面內所有向量的“相伴函數”構成的集合為S．
（1）設h（x）=cos（x+
π
6
）-2cos（x+a）（a∈R），求證：h（x）∈S；
（2）求（1）中函數h（x）的“相伴向量”模的取值范圍；
（3）已知點M（a，b）（b≠0）滿足：(a-
3
)2+(b-1)2=1上一點，向量
OM
的“相伴函數”f（x）在x=x0處取得最大值．當點M運動時，求tan2x0的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：

（2012•上海）定義向量
OM
=（a，b）的“相伴函數”為f（x）=asinx+bcosx，函數f（x）=asinx+bcosx的“相伴向量”為
OM
=（a，b）（其中O為坐標原點）．記平面內所有向量的“相伴函數”構成的集合為S．
（1）設g（x）=3sin（x+
π
2
）+4sinx，求證：g（x）∈S；
（2）已知h（x）=cos（x+α）+2cosx，且h（x）∈S，求其“相伴向量”的模；
（3）已知M（a，b）（b≠0）為圓C：（x-2）2+y2=1上一點，向量
OM
的“相伴函數”f（x）在x=x0處取得最大值．當點M在圓C上運動時，求tan2x0的取值范圍．

查看答案和解析>>

科目：高中數學 來源：高考真題 題型：解答題

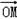定義向量=（a，b）的“相伴函數”為f（x）=asinx+bcosx，函數f（x）=asinx+bcosx的“相伴向量”為=（a，b）（其中O為坐標原點），記平面內所有向量的“相伴函數”構成的集合為S。
（1）設g（x）=3sin（x+）+4sinx，求證：g（x）∈S；
（2）已知h（x）=cos（x+α）+2cosx，且h（x）∈S，求其“相伴向量”的模；
（3）已知M（a，b）（b≠0）為圓C：（x-2）2+y2=1上一點，向量的“相伴函數”f（x）在x=x0處取得最大值，當點M在圓C上運動時，求tan2x0的取值范圍。

查看答案和解析>>

科目：高中數學 來源： 題型：

已知向量a=(cos(x+)，1)，b=(cos(x+，)，c=(cos(x+)，0)，f(x)=a·b，g(x)=a·c.

(Ⅰ)要得到了y=f(x)的圖像，只需要把g(x)的圖像經過怎樣的變化?

(Ⅱ)設h(x)=f(x)+g(x)，求h(x)的最小正周期及單調遞增區間.

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 91精产国品一二三区在线观看 | 日本一区二区视频在线 | 一区二区三区回区在观看免费视频 | 久久久二 | 久久伊人在| 色综合色综合网色综合 | 久久三区 | 久热av中文字幕 | 国产精品视频一区二区噜噜 | 亚洲一区国产精品 | 久草新在线 | 99精品欧美一区二区蜜桃免费 | 成人免费毛片嘿嘿连载视频 | 国产高清精品在线 | 精品国产成人 | 亚洲成人av在线 | 精品国产不卡一区二区三区 | 国产精品对白一区二区三区 | av在线免费播放 | 在线播放国产一区二区三区 | 91免费国产 | 欧美激情精品久久久久 | 在线视频久| 国产成人午夜精品影院游乐网 | 久久精品欧美一区二区三区不卡 | 久久婷婷麻豆国产91天堂 | 欧美极品一区二区 | 国产成人免费在线 | 久久精品影视 | av在线一区二区三区 | 精品一区二区av | 国产一区二区三区免费观看 | 一区二区在线视频免费观看 | 日本精品视频 | 亚洲国产福利在线 | 视频一区 中文字幕 | 91精品一区二区三区在线观看 | 成人涩涩日本国产一区 | 欧美精品 在线观看 | 久久久久久久久99精品 | 超碰香蕉 |