
 已知一列橢圓
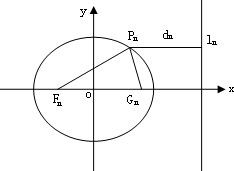
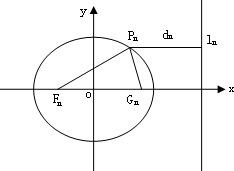
已知一列橢圓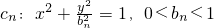 .n=1,2….若橢圓Cn上有一點Pn,使Pn到右準線ln的距離dn是{pnFn}與{PnGn}的等差中項,其中Fn、Gn分別是Cn的左、右焦點.
.n=1,2….若橢圓Cn上有一點Pn,使Pn到右準線ln的距離dn是{pnFn}與{PnGn}的等差中項,其中Fn、Gn分別是Cn的左、右焦點.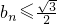 (n≥1);
(n≥1);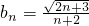 ,并用Sn表示△PnFnGn的面積,試證:S1<S2且Sn>Sn+1(n≥3).
,并用Sn表示△PnFnGn的面積,試證:S1<S2且Sn>Sn+1(n≥3). ,則右準線方程為
,則右準線方程為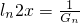 .
.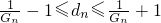 .
. ,解之得:
,解之得: .
.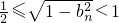 .從而對任意
.從而對任意 .
.
 .因{FnGn}=2Gn,
.因{FnGn}=2Gn, .
. .從而易知函數f(c)在
.從而易知函數f(c)在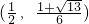 內是增函數.
內是增函數. 內是減函數.
內是減函數.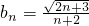 ,
,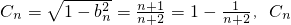 是增數列.
是增數列. .
. ,則右準線方程為
,則右準線方程為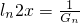 .由題設條件能推出
.由題設條件能推出 .即
.即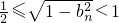 .從而證出對任意
.從而證出對任意


科目:高中數學 來源: 題型:
 已知一列橢圓cn:x2+
已知一列橢圓cn:x2+| y2 | ||
|
| ||
| 2 |
| ||
| n+2 |
查看答案和解析>>
科目:高中數學 來源:重慶市高考真題 題型:證明題
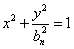 , 0<bn<1,n=1,2,…,若橢圓Cn上有一點Pn,使Pn到右準線ln的距離dn是|PnFn|與|PnGn|的等差中項,其中Fn、Gn分別是Cn的左、右焦點,
, 0<bn<1,n=1,2,…,若橢圓Cn上有一點Pn,使Pn到右準線ln的距離dn是|PnFn|與|PnGn|的等差中項,其中Fn、Gn分別是Cn的左、右焦點,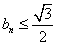 (n≥1);
(n≥1);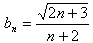 ,并用Sn表示△PnFnGn的面積,試證:S1<S2且Sn>Sn+1(n≥3)。
,并用Sn表示△PnFnGn的面積,試證:S1<S2且Sn>Sn+1(n≥3)。 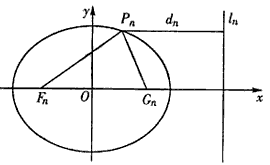
查看答案和解析>>
科目:高中數學 來源: 題型:
已知一列橢圓Cn:x2+![]() =1. 0<bn<1,n=1,2.
=1. 0<bn<1,n=1,2.![]() .若橢圓C上有一點Pn使Pn到右準線
.若橢圓C上有一點Pn使Pn到右準線![]() n的距離d.是|PnFn|與|PnCn|的等差中項,其中Fn、Cn分別是Cn的左、右焦點.
n的距離d.是|PnFn|與|PnCn|的等差中項,其中Fn、Cn分別是Cn的左、右焦點.
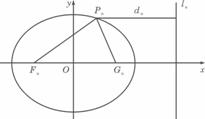 (Ⅰ)試證:bn≤
(Ⅰ)試證:bn≤![]() (n≥1);
(n≥1);
(Ⅱ)取bn=![]() ,并用SA表示
,并用SA表示![]() PnFnGn的面積,試證:S1<S1且Sn<Sn+3 (n≥3).
PnFnGn的面積,試證:S1<S1且Sn<Sn+3 (n≥3).
查看答案和解析>>
科目:高中數學 來源:2006年重慶市高考數學試卷(理科)(解析版) 題型:解答題
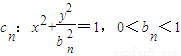 .n=1,2….若橢圓Cn上有一點Pn,使Pn到右準線ln的距離dn是{pnFn}與{PnGn}的等差中項,其中Fn、Gn分別是Cn的左、右焦點.
.n=1,2….若橢圓Cn上有一點Pn,使Pn到右準線ln的距離dn是{pnFn}與{PnGn}的等差中項,其中Fn、Gn分別是Cn的左、右焦點. (n≥1);
(n≥1);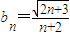 ,并用Sn表示△PnFnGn的面積,試證:S1<S2且Sn>Sn+1(n≥3).
,并用Sn表示△PnFnGn的面積,試證:S1<S2且Sn>Sn+1(n≥3).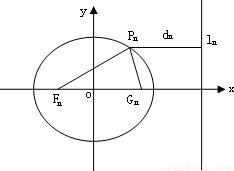
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com