【題目】已知函數f(x)＝log2(1－x)，g(x)＝log2(x＋1)，設F(x)＝f(x)－g(x)．
(1)判斷函數F(x)的奇偶性；
(2)證明函數F(x)是減函數．
【答案】（1）奇函數．（2）見解析
【解析】試題分析：（1）先研究函數定義域，關于原點對稱，再研究F(－x)與F(x)關系：相反，根據奇函數定義確定奇偶性（2）根據定義，作差，根據對數性質進行化簡，再比較真數大小，確定差的符號，最后根據減函數定義進行判斷.
試題解析：(1)F(x)＝f(x)－g(x)＝log2(1－x)－log2(x＋1)＝log2
.
由
得－1＜x＜1.∴函數F(x)的定義域為(－1,1)．
∴函數F(x)的定義域關于原點對稱，
又∵F(－x)＝log2
＝－log2＝－F(x)．
∴函數F(x)為奇函數．
(2)由(1)知函數F(x)的定義域為(－1,1)，
任取－1＜x1＜x2＜1，則log2(
)－log2(
)＝log2
＝log2(
)，
又(1－x1＋x2－x1x2)－(1＋x1－x2－x1x2)＝2(x2－x1)＞0，所以＞1，
所以log2()－log2()＞0，即log2()＞log2()，
所以函數F(x)是減函數．
導學與測試系列答案
新非凡教輔沖刺100分系列答案科目：高中數學 來源： 題型：
【題目】設函數f（x）=x2-4|x|-5．
（Ⅰ）畫出y=f（x）的圖象；
（Ⅱ）設A={x|f（x）≥7}，求集合A；
（Ⅲ）方程f（x）=k+1有兩解，求實數k的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
中，
，且點
在直線
上．
⑴求數列的通項公式；
⑵若函數
（
，且
），求函數
的最小值；
⑶設
，
表示數列
的前
項和，試問：是否存在關于
的整式
，使得
對于一切不小于2的自然數
恒成立？若存在，寫出
的解析式，并加以證明；若不存在，試說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某理科考生參加自主招生面試，從7道題中（4道理科題3道文科題）不放回地依次任取3道作答.
（1）求該考生在第一次抽到理科題的條件下，第二次和第三次均抽到文科題的概率；
（2）規定理科考生需作答兩道理科題和一道文科題，該考生答對理科題的概率均為
，答對文科題的概率均為
，若每題答對得10分，否則得零分.現該生已抽到三道題（兩理一文），求其所得總分
的分布列與數學期望
.
查看答案和解析>>
科目：高中數學 來源： 題型：
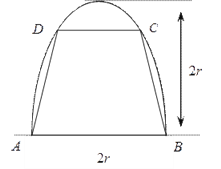
【題目】如圖，有一塊半橢圓形鋼板，其長半軸為
，短半軸為
，計劃將此鋼板切割成等腰梯形的形狀，下底
是半橢圓的短軸，上底
的端點在橢圓上，記
，梯形面積為
．
(Ⅰ)求面積關于變量
的函數表達式，并寫出定義域；
(Ⅱ)求面積的最大值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
