
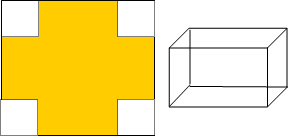
如圖所示,現有一邊長為6的正方形鐵板,如果從鐵板的四個角各截出去一個相同的小正方形,做成一個長方體形的無蓋容器為使其容積最大,截下的小正方形邊長應為多少?

當截下的正方形邊長為1時,容積最大.
【解析】本題是考察導數應用的題目先設截下的小正方形邊長x,然后建立容積V(x)的關系式,再求導,根據導數等于零,確定最值一般地在應用題中,一般考察的都是單峰函數,導數等于零的位置只有一個,它就是要求的最值位置
解:設截下的小正方形邊長x,容器容積為
V(x),則做成長方體形無蓋容器底面邊長
為8-2x,高為X,于是
V(x)=(6-2x)2 x,0<x<3
即 V(x)=4x3 -24x2+36x,0<x<3
有 V'(x)=12x2-48x+36
令V'(x)=0,即令12x2-48x+36=0
解得x1=1,x2=3(舍去)
當0<x<1時,V'(x)>0;當1<x<3時,V'(x)<0
因此x=1是極大值點,且在區間(1,3)內,是唯一的極值點,所以x=1是V(x)的最大值點
即當截下的正方形邊長為1時,容積最大


科目:高中數學 來源:山東省濟南世紀英華實驗學校2011-2012學年高二下學期期中考試數學理科試題 題型:044
如圖所示,現有一邊長為6的正方形鐵板,如果從鐵板的四個角各截出去一個相同的小正方形,做成一個長方體形的無蓋容器.為使其容積最大,截下的小正方形邊長應為多少?
查看答案和解析>>
科目:高中數學 來源:2012-2013學年浙江省紹興市高一下學期期中考試理科數學試卷(解析版) 題型:解答題
作為紹興市2013年5.1勞動節系列活動之一的花卉展在鏡湖濕地公園舉行.現有一占地1800平方米的矩形地塊,中間三個矩形設計為花圃(如圖),種植有不同品種的觀賞花卉,周圍則均是寬為1米的賞花小徑,設花圃占地面積為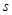 平方米,矩形一邊的長為
平方米,矩形一邊的長為 米(如圖所示)
米(如圖所示)

(1)試將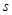 表示為
表示為 的函數;
的函數;
(2)問應該如何設計矩形地塊的邊長,使花圃占地面積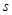 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年浙江省紹興市高一下學期期中考試文科數學試卷(解析版) 題型:解答題
作為紹興市2013年5.1勞動節系列活動之一的花卉展在鏡湖濕地公園舉行.現有一占地1800平方米的矩形地塊,中間三個矩形設計為花圃(如圖),種植有不同品種的觀賞花卉,周圍則均是寬為1米的賞花小徑,設花圃占地面積為 平方米,矩形一邊的長為
平方米,矩形一邊的長為 米(如圖所示)
米(如圖所示)

(1)試將 表示為
表示為 的函數;
的函數;
(2)問應該如何設計矩形地塊的邊長,使花圃占地面積 取得最大值.
取得最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com