【題目】已知函數
的最大值為2.
（Ⅰ）求函數
在
上的單調遞減區間；
（Ⅱ）
中，角
，
，
所對的邊分別是
，
，
，且
，
，若
，求的面積.
【答案】（1）
；（2）
.
【解析】試題分析：（1）將
解析式輔助角化為一個角的正弦函數，由正弦函數的值域表示出
的最大值，由已知最大值為
列出關于
的方程，求出方程的解得到
的值，進而確定出
解析式，由正弦定理的遞減區間為
，列出關于
的不等式，求出不等式的解集即可得到
在
上的單調遞減區間；（2）由（1）確定的
解析式化簡
，再利用正弦定理化簡，得出
①， 利用余弦定理化簡，得到
②，將①代入②求出
的值，再由
的值，利用三角形的面積公式即可，求出三角形
的面積.
試題解析：（1）由題意，
的最大值
，所以
，
而
，于是
，
.
為遞減函數，則
滿足
（
）.
即
（）.
所以在
上的單調遞減區間為
.
（2）設
的外接圓半徑為
，由題意，得
.
化簡
，得
.
由正弦定理，得
，
.①
由余弦定理，得
，即
.②
將①式代入②，得
.
解得
，或
（舍去），
.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ax﹣lnx﹣1，若曲線y=f（x）在點（2，f（2））處的切線與直線2x+y﹣1=0垂直．
（1）求a的值；
（2）函數g（x）=f（x）﹣m（x﹣1）（m∈R）恰有兩個零點x1 ， x2（x1＜x2），求函數g（x）的單調區間及實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設定義域為R的函數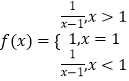 
，若關于x的方程f2（x）+bf（x）+c=0有三個不同的解x1 ， x2 ， x3 ， 則 
的值是（ ）
A.1
B.3
C.5
D.10
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】十八屆五中全會公報指出：努力促進人口均衡發展，堅持計劃生育的基本國策，完善人口發展戰略，全面實施一對夫婦可生育兩個孩子的政策，提高生殖健康、婦幼保健、托幼等公共服務水平．為了解適齡公務員對放開生育二胎政策的態度，某部門隨機調查了100位30到40歲的公務員，得到情況如下表：
男公務員 | 女公務員 | |
生二胎 | 40 | 20 |
不生二胎 | 20 | 20 |
（1）是否有95%以上的把握認為“生二胎與性別有關”，并說明理由；
（2）把以上頻率當概率，若從社會上隨機抽取3位30到40歲的男公務員，記其中生二胎的人數為X，求隨機變量X的分布列，數學期望．
附：K2= 
P（K2≥k0） | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】商品在近30天內每件的銷售價格P（元）與時間t（天）的函數關系p= 
該商品的日銷售量Q（件）時間t（天）的函數關系Q=﹣t+40（0＜t≤30，t∈N*）
求該商品的日銷售額的最大值，并指出日銷售額最大一天是30天中的第幾天？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
的上下兩個焦點分別為
，過點
與
軸垂直的直線交橢圓
于
兩點， 
的面積為
，橢圓
的離心率為
．
（1）求橢圓
的標準方程；
（2）已知
為坐標原點，直線
與
軸交于點
，與橢圓
交于
兩個不同的點，若
，求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在正方體ABCDA1B1C1D1中，M為DD1的中點，O為四邊形ABCD的中心，P為棱A1B1上任一點，則異面直線OP與MA所成的角為（ ）
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在直角坐標系中
中，曲線
的參數方程為
為參數， 
）. 以坐標原點為極點， 
軸正半軸為極軸建立極坐標系，已知直線
的極坐標方程為
.
（1）設
是曲線
上的一個動點，當
時，求點
到直線
的距離的最大值；
（2）若曲線
上所有的點均在直線
的右下方，求
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
