【題目】（1）用輾轉相除法求228與1995的最大公約數．
（2）用秦九韶算法求多項式f（x）=
+
-8x+5在x=2時的值。
【答案】（1）57（2）101
【解析】
試題分析：（1）用較大的數字除以較小的數字，得到商和余數，然后再用上一式中的除數和得到的余數中較大的除以較小的，以此類推，當整除時，就得到要求的最大公約數；（2）首先把一個n次多項式f（x）寫成（…（（a[n]x+a[n-1]）x+a[n-2]）x+…+a[1]）x+a[0]的形式，然后化簡，求n次多項式f（x）的值就轉化為求n個一次多項式的值，求出函數的值
試題解析：（1）解：1995=228
8+171， 228=171
1+57， 171=57
3
因此57是1995與228的最大公約數。
（2）解： f（x）=
+
-8x+5=（（（（3x+0）x+2）x+0）x-8）x+5
=3, 
=3
2=6, 
=6
2+2=14, 
=14
2=28
=28
2-8=48, 
=48
2+5=101
所以，當x=2時，多項式的值是101．
科目：高中數學 來源： 題型：
【題目】若一系列函數的解析式相同，值域相同，但其定義域不同，則稱這些函數為“同族函數”，那么y=x2 ， 值域為{1，9}的“同族函數”共有（ ）
A.7個
B.8個
C.9個
D.10個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線
,半徑為
的圓
與
相切，圓心在
軸上且在直線
的右上方．
（1）求圓的方程；
（2）若直線過點
且與圓
交于
兩點（
在
軸上方,B在軸下方），問在
軸正半軸上是否存在定點
,使得軸平分
？若存在，請求出點
的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設a1，d為實數，首項為a1，公差為d的等差數列{an}的前n項和為Sn，滿足S5S6＋15＝0．
（1）若S5＝5，求S6及a1；
（2）求d的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校研究性學習小組對該校高三學生視力情況進行調查，在高三的全體1000名學生中隨機抽取了100名學生的體檢表，并得到如圖的頻率分布直方圖.
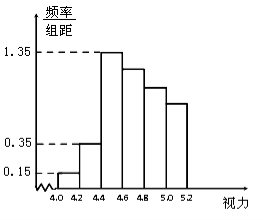
（1）若直方圖中后四組的頻數成等差數列，試估計全年級視力在5.0以下的人數；
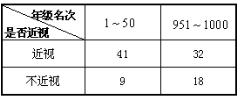
（2）學習小組成員發現，學習成績突出的學生，近視的比較多，為了研究學生的視力與學習成績是否有關系，對年級名次在1～50名和951～1000名的學生進行了調查，得到右表中數據，根據表中的數據，能否在犯錯的概率不超過0.05的前提下認為視力與學習成績有關系?
（3）在（2）中調查的100名學生中，按照分層抽樣在不近視的學生中抽取了9人，進一步調查他們良好的護眼習慣，并且在這9人中任取3人，記名次在1～50的學生人數為
，求的分布列和數學期望.
附：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地空氣中出現污染，須噴灑一定量的去污劑進行處理.據測算，每噴灑
個單位的去污劑，空氣中釋放的濃度
（單位：毫克/立方米）隨著時間
單位：天）變化的函數關系式，近似為
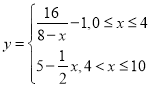,若多次噴灑，則某一時刻空氣中的去污劑濃度為每次投放的去污劑在相應時刻所釋放的濃度之和. 由實驗知，當空氣中去污劑的濃度不低于
（毫克/立方米）時，它才能起到去污作用.
（1）若一次噴灑
個單位的去污劑，則去污時間可達幾天？
（2）若第一次噴灑
個單位的去污劑，
天后再嗩灑
個單位的去污劑，要使接來的
天中能夠持續有效去污，試求
的最小值（精確到
，參考數據:
取
）.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com