
【題目】如圖,正四面體ABCD的邊長等于2,點A,E位于平面BCD的兩側,且![]() ,點P是AC的中點.
,點P是AC的中點.
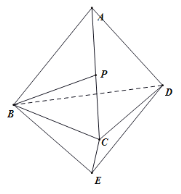
(1)求證:![]() 平面
平面![]()
(2)求BP與平面![]() 所成的角的正弦值
所成的角的正弦值
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)首先取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,根據已知條件易證
,根據已知條件易證![]() 與
與![]() 相似,從而得到
相似,從而得到![]() ,再利用線面平行的判定證明即可.
,再利用線面平行的判定證明即可.
(2)取![]() 中點
中點![]() ,連接
,連接![]() ,根據題意易證
,根據題意易證![]() 平面
平面![]() ,設
,設![]() 與平面
與平面![]() 所成角為
所成角為![]() ,
,![]() 與
與![]() 所成的角為
所成的角為![]() ,得到
,得到![]() ,再利用向量法即可得到答案.
,再利用向量法即可得到答案.
(1)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,如圖所示:
,如圖所示:
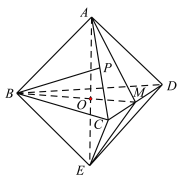
設![]() 在平面
在平面![]() 上的射影為
上的射影為![]() ,即
,即![]() 平面
平面![]() ,
,
![]() ,
,
所以![]() 為
為![]() 外心,
外心,
![]() ,同理可證
,同理可證![]() 在平面
在平面![]() 上的射影為
上的射影為![]() ,
,
即![]() 平面
平面![]() ,所以
,所以![]() 三點共線,
三點共線,
即![]() ,所以四邊形
,所以四邊形![]() 為平面四邊形,
為平面四邊形,
且![]() 為
為![]() 的中心,因為正四面體
的中心,因為正四面體![]() 的邊長等于
的邊長等于![]() ,
,
所以![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
(2)取![]() 中點
中點![]() ,連接
,連接![]() ,如圖所示:
,如圖所示:
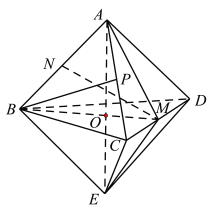
因為正四面體![]() ,
,
所以![]() ,
,![]() ,又因為
,又因為![]() ,
,
所以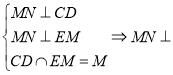 平面
平面![]() ,
,
設![]() 與平面
與平面![]() 所成角為
所成角為![]() ,
,
![]() 與
與![]() 所成的角為
所成的角為![]() ,則
,則![]() ,
,
設![]() 為一組基底,
為一組基底,
則![]() ,
,![]()
所以![]() ,
,
![]()
![]() .
.
因為![]() ,
,
所以![]() .
.
又因為![]() ,
,![]() ,
,
所以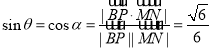 ,
,
即![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】某地區城鄉居民儲蓄存款年底余額(單位:億元)如圖所示,下列判斷一定不正確的是( )
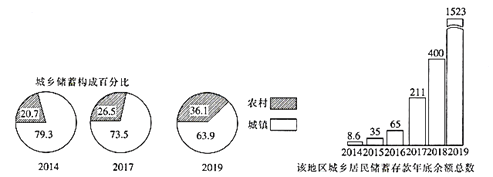
A.城鄉居民儲蓄存款年底余額逐年增長
B.農村居民的存款年底余額所占比重逐年上升
C.到2019年農村居民存款年底總余額已超過了城鎮居民存款年底總余額
D.城鎮居民存款年底余額所占的比重逐年下降
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】紅鈴蟲(Pectinophora gossypiella)是棉花的主要害蟲之一,其產卵數與溫度有關.現收集到一只紅鈴蟲的產卵數y(個)和溫度x(℃)的8組觀測數據,制成圖1所示的散點圖.現用兩種模型①![]() ,②
,②![]() 分別進行擬合,由此得到相應的回歸方程并進行殘差分析,進一步得到圖2所示的殘差圖.
分別進行擬合,由此得到相應的回歸方程并進行殘差分析,進一步得到圖2所示的殘差圖.
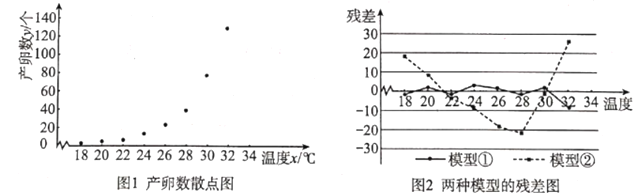
根據收集到的數據,計算得到如下值:
|
|
|
|
|
|
|
25 | 2.89 | 646 | 168 | 422688 | 48.48 | 70308 |
表中![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(1)根據殘差圖,比較模型①、②的擬合效果,應選擇哪個模型?并說明理由;
(2)根據(1)中所選擇的模型,求出y關于x的回歸方程(系數精確到0.01),并求溫度為34℃時,產卵數y的預報值.
(參考數據:![]() ,
,![]() ,
,![]() ,
,![]() )
)
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為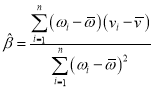 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】共享單車是指由企業在校園、公交站點、商業區、公共服務區等場所提供的自行車單車共享服務,由于其依托“互聯網+”,符合“低碳出行”的理念,已越來越多地引起了人們的關注.某部門為了對該市共享單車加強監管,隨機選取了50人就該城市共享單車的推行情況進行問卷調查,并將問卷中的這50人根據其滿意度評分值(百分制)按照![]() ,
,![]() ,……
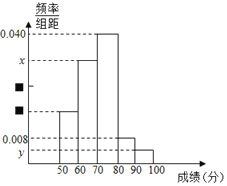
,……![]() 分成5組,根據下面尚未完成并有局部污損的頻率分布表和頻率分布直方圖(如圖所示),計算
分成5組,根據下面尚未完成并有局部污損的頻率分布表和頻率分布直方圖(如圖所示),計算![]() ,
,![]() ,
,![]() ,
,![]() 的值分別為( )
的值分別為( )
組別 | 分組 | 頻數 | 頻率 |
第1組 |
| 8 | 0.16 |
第2組 |
|
| ■ |
第3組 |
| 20 | 0.40 |
第4組 |
| ■ | 0.08 |
第5組 |
| 2 |
|
合計 | ■ | ■ |
A.16,0.04,0.032,0.004B.16,0.4,0.032,0.004
C.16,0.04,0.32,0.004D.12,0.04,0.032,0.04
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,用一個半徑為10厘米的半圓紙片卷成一個最大的無底圓錐,放在水平桌面上,被一陣風吹倒.
(1)求該圓錐的表面積![]() 和體積
和體積![]() ;
;
(2)求該圓錐被吹倒后,其最高點到桌面的距離![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】點![]() 與定點
與定點![]() 的距離和它到直線
的距離和它到直線![]() 的距離的比是常數
的距離的比是常數![]() .
.
(Ⅰ)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)過坐標原點![]() 的直線交軌跡
的直線交軌跡![]() 于
于![]() ,
,![]() 兩點,軌跡
兩點,軌跡![]() 上異于
上異于![]() ,
,![]() 的點
的點![]() 滿足直線
滿足直線![]() 的斜率為
的斜率為![]() .
.
(ⅰ)求直線![]() 的斜率;
的斜率;
(ⅱ)求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查某社區居民每天參加健身的時間,某機構在該社區隨機采訪男性、女性各50名,其中每人每天的健身時間不少于1小時稱為“健身族”,否則稱其為"非健身族”,調查結果如下:
健身族 | 非健身族 | 合計 | |
男性 | 40 | 10 | 50 |
女性 | 30 | 20 | 50 |
合計 | 70 | 30 | 100 |
(1)若居民每人每天的平均健身時間不低于70分鐘,則稱該社區為“健身社區”. 已知被隨機采訪的男性健身族,男性非健身族,女性健身族,女性非健身族每人每天的平均健分時間分別是1.2小時,0.8小時,1.5小時,0.7小時,試估計該社區可否稱為“健身社區”?
(2)根據以上數據,能否在犯錯誤的概率不超過5%的情況下認為“健身族”與“性別”有關?
參考公式: 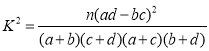 ,其中
,其中![]() .
.
參考數據:
| 0. 50 | 0. 40 | 0. 25 | 0. 05 | 0. 025 | 0. 010 |
| 0. 455 | 0. 708 | 1. 321 | 3. 840 | 5. 024 | 6. 635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知橢圓![]() 過點
過點![]() ,
,![]() ,
,![]() 是兩個焦點.以橢圓
是兩個焦點.以橢圓![]() 的上頂點
的上頂點![]() 為圓心作半徑為
為圓心作半徑為![]() 的圓,
的圓,
(1)求橢圓![]() 的方程;
的方程;
(2)存在過原點的直線![]() ,與圓
,與圓![]() 分別交于
分別交于![]() ,
,![]() 兩點,與橢圓
兩點,與橢圓![]() 分別交于
分別交于![]() ,
,![]() 兩點(點
兩點(點![]() 在線段
在線段![]() 上),使得
上),使得![]() ,求圓
,求圓![]() 半徑
半徑![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com