
【題目】如圖甲是某商店2018年(按360天計算)的日盈利額(單位:萬元)的統計圖.
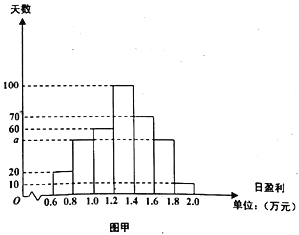
(1)請計算出該商店2018年日盈利額的平均值(精確到0.1,單位:萬元):
(2)為了刺激消費者,該商店于2019年1月舉行有獎促銷活動,顧客凡購買一定金額的高品后均可參加抽獎.隨著抽獎活動的有效開展,參與抽獎活動的人數越來越多,該商店對前5天抽獎活動的人數進行統計如下表:(![]() 表示第
表示第![]() 天參加抽獎活動的人數)
天參加抽獎活動的人數)
| 1 | 2 | 3 | 4 | 5 |
| 50 | 60 | 70 | 80 | 100 |
經過進一步統計分析,發現![]() 與
與![]() 具有線性相關關系.
具有線性相關關系.
(ⅰ)根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() :
:
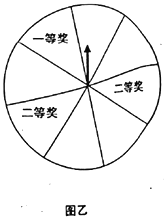
(ⅱ)該商店采取轉盤方式進行抽獎(如圖乙),其中轉盤是個八等分的圓.每位顧客最多兩次抽獎機會,若第一次抽到獎,則抽獎終止,若第一次未抽到獎,則再提供一次抽獎機會.抽到一等獎的獎品價值128元,抽到二等獎的獎品價值32元.若該商店此次抽獎活動持續7天,試估計該商店在此次抽獎活動結束時共送出價值為多少元的獎品(精確到0.1,單位:萬元)?
(3)用(1)中的2018年日盈利額的平均值去估計當月(共31天)每天的日盈利額.若商店每天的固定支出約為1000元,促銷活動日的日盈利額比平常增加20%,則該商店當月的純利潤約為多少萬元?(精確到0.1,純利潤=盈利額-固定支出-抽獎總獎金數)
參考公式及數據: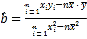 ,
,![]() ,
,![]() ,
,![]() .
.
【答案】(1)1.3(萬元);(2)(ⅰ)![]()
![]() ,(ⅱ)2.3萬元;(3)36.7萬元
,(ⅱ)2.3萬元;(3)36.7萬元
【解析】
(1)由總天數360列方程,求出統計圖中![]() 的值,然后計算日盈利額的平均值即可;(2)(ⅰ)算出
的值,然后計算日盈利額的平均值即可;(2)(ⅰ)算出![]() ,結合參考公式和數據,即可求出線性回歸方程;(ⅱ)由轉盤分布可知,顧客每次抽到一二三等獎的概率均為
,結合參考公式和數據,即可求出線性回歸方程;(ⅱ)由轉盤分布可知,顧客每次抽到一二三等獎的概率均為![]() ,無獎的概率為
,無獎的概率為![]() ,設一位參加抽獎的顧客獲得的獎品價值
,設一位參加抽獎的顧客獲得的獎品價值![]() 元,則
元,則![]() 的取值可能為128、32、0,然后分別求出其概率,列出分布列求出方程,由線性回歸方程估算出第6、7兩天的人數,然后加上前5天人數得到抽獎總人數,再乘以每位顧客中獎獎品價值的期望值即可;(3)由(1)中的日盈利額的平均值乘以天數31,再加上促銷日額外多出的盈利額即為總盈利額,再減去固定總支出,以及(2)中得出的抽獎總獎金數即可.
的取值可能為128、32、0,然后分別求出其概率,列出分布列求出方程,由線性回歸方程估算出第6、7兩天的人數,然后加上前5天人數得到抽獎總人數,再乘以每位顧客中獎獎品價值的期望值即可;(3)由(1)中的日盈利額的平均值乘以天數31,再加上促銷日額外多出的盈利額即為總盈利額,再減去固定總支出,以及(2)中得出的抽獎總獎金數即可.
(1)由題意可知:![]() ,解得
,解得![]() .
.
所以日盈利額的平均值為
![]()
![]() (萬元).
(萬元).
(2)(ⅰ)![]() ,
,![]()
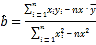
![]() ,
,
![]() ,
,
所以![]()
![]() .
.
(ⅱ)由轉盤分布可知,顧客每次抽到一二三等獎的概率均為![]() ,無獎的概率為
,無獎的概率為![]()
設一位參加抽獎的顧客獲得的獎品價值![]() 元,則
元,則![]() 的分布列為:
的分布列為:
![]() ,
,![]() ,
,![]() ,
,
| 128 | 32 | 0 |
|
|
|
|
故![]() (元)
(元)
由于![]() 關于
關于![]() 的線性回歸方程為
的線性回歸方程為![]()
![]() ,得
,得![]() 時
時![]() ,
,![]() 時
時![]() ,則此次活動參加抽獎的總人數約為
,則此次活動參加抽獎的總人數約為![]() ,
,
![]() 該商店在此次抽獎活動結束時共送出的獎品總價值為
該商店在此次抽獎活動結束時共送出的獎品總價值為![]() 萬元
萬元
(3)當月的純利潤約為![]() (萬元),故該商店當月的純利潤約為36.7萬元.
(萬元),故該商店當月的純利潤約為36.7萬元.


 口算題天天練系列答案
口算題天天練系列答案科目:高中數學 來源: 題型:
【題目】如圖,某隧道的剖面圖是由半圓及矩形![]() 組成,交通部門擬在隧道頂部安裝通風設備(視作點
組成,交通部門擬在隧道頂部安裝通風設備(視作點![]() ),為了固定該設備,計劃除從隧道最高點
),為了固定該設備,計劃除從隧道最高點![]() 處使用鋼管垂直向下吊裝以外,再在兩側自
處使用鋼管垂直向下吊裝以外,再在兩側自![]() 兩點分別使用鋼管支撐.已知道路寬
兩點分別使用鋼管支撐.已知道路寬![]() ,設備要求安裝在半圓內部,所使用的鋼管總長度為
,設備要求安裝在半圓內部,所使用的鋼管總長度為![]() .
.
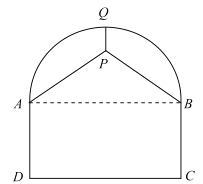
(1)①設![]() ,將
,將![]() 表示為關于
表示為關于![]() 的函數;
的函數;
②設![]() ,將
,將![]() 表示為關于
表示為關于![]() 的函數;
的函數;
(2)請選用(1)中的一個函數關系式,說明如何設計,所用的鋼管材料最省?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4—4:坐標系與參數方程]:在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (t為參數,
(t為參數,![]() ),以坐標原點為極點,以x軸的非負半軸為極軸,建立極坐標系,曲線C的極坐標方程為
),以坐標原點為極點,以x軸的非負半軸為極軸,建立極坐標系,曲線C的極坐標方程為![]() ,已知直線
,已知直線![]() 與曲線C交于不同的兩點A,B.
與曲線C交于不同的兩點A,B.
(1)求直線![]() 的普通方程和曲線C的直角坐標方程;
的普通方程和曲線C的直角坐標方程;
(2)設P(1,2),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知下列命題:
①在線性回歸模型中,相關指數![]() 越接近于1,表示回歸效果越好;
越接近于1,表示回歸效果越好;
②兩個變量相關性越強,則相關系數r就越接近于1;
③在回歸直線方程![]() 中,當解釋變量
中,當解釋變量![]() 每增加一個單位時,預報變量
每增加一個單位時,預報變量![]() 平均減少0.5個單位;
平均減少0.5個單位;
④兩個模型中殘差平方和越小的模型擬合的效果越好.
⑤回歸直線![]() 恒過樣本點的中心
恒過樣本點的中心![]() ,且至少過一個樣本點;
,且至少過一個樣本點;
⑥若![]() 的觀測值滿足
的觀測值滿足![]() ≥6.635,我們有99%的把握認為吸煙與患肺病有關系,那么在100個吸煙的人中必有99人患有肺病;
≥6.635,我們有99%的把握認為吸煙與患肺病有關系,那么在100個吸煙的人中必有99人患有肺病;
⑦從統計量中得知有95%的把握認為吸煙與患肺病有關系,是指有5%的可能性使得推斷出現錯誤. 其中正確命題的序號是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某投資公司計劃投資A,B兩種金融產品,根據市場調查與預測,A產品的利潤y1與投資金額x的函數關系為y1=18-![]() ,B產品的利潤y2與投資金額x的函數關系為y2=
,B產品的利潤y2與投資金額x的函數關系為y2=![]() (注:利潤與投資金額單位:萬元).
(注:利潤與投資金額單位:萬元).
(1)該公司已有100萬元資金,并全部投入A,B兩種產品中,其中x萬元資金投入A產品,試把A,B兩種產品利潤總和表示為x的函數,并寫出定義域;
(2)在(1)的條件下,試問:怎樣分配這100萬元資金,才能使公司獲得最大利潤?其最大利潤為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的左焦點為
的左焦點為![]() ,右頂點為
,右頂點為![]() ,離心率為
,離心率為![]() .已知
.已知![]() 是拋物線
是拋物線![]() 的焦點,
的焦點, ![]() 到拋物線的準線
到拋物線的準線![]() 的距離為
的距離為![]() .
.
(I)求橢圓的方程和拋物線的方程;
(II)設![]() 上兩點
上兩點![]() ,
, ![]() 關于
關于![]() 軸對稱,直線
軸對稱,直線![]() 與橢圓相交于點
與橢圓相交于點![]() (
(![]() 異于點
異于點![]() ),直線
),直線![]() 與
與![]() 軸相交于點
軸相交于點![]() .若
.若![]() 的面積為
的面積為![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com