分析:(Ⅰ)求出g(x),
loga=f(x)在[2,6]上有實數解,求出t的表達式,利用導數確定t 的范圍;
(Ⅱ)a=e求出
h(x)=g(x)-(x≥0),利用導數推出是增函數,求出最小值,即可求函數h(x)的最大值;
(Ⅲ)利用放縮法,求出
| n |
 |
| k=1 |
g(a-k)的取值范圍,最后推出小于
即可.
解答:解:(Ⅰ)由條件可知:t=(1+x)(2x
2-5x+5),在x∈[0,1)上有解.
t'=6x(x-1),當x∈[0,1)時,t'(x)<0,所以t(x)在[0,1)上單調遞減.t(1)<t(x)≤t(0),即4<t≤5.(4分)
(Ⅱ)f(x)的定義域為(-1,1),
g(x)=f-1(x)=(x∈R),
當a=e時,
h(x)=-(x≥0),所以
h′(x)=≤0,
所以h(x)在[0,+∞)上單調遞減.所以,x≥0時,h(x)
max=h(0)=0;(8分)
(Ⅲ)由(Ⅱ)的啟示可以設
G(x)=g(x)-x,(x≥0)則
G′(x)=g′(x)-=≤0,
所以G(x)在[0,+∞)上單調遞減,
當x>0時,G(x)<G(0)=0,即
g(x)<x所以
| n |
 |
| k=1 |
g(a-k)<(+++)=.<.(16分)
點評:本小題考查函數、反函數、方程、不等式、導數及其應用等基礎知識,考查化歸、分類整合等數學思想方法,以及推理論證、分析與解決問題的能力.






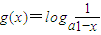 ,記F(x)=2f(x)+g(x)
,記F(x)=2f(x)+g(x)