已知甲盒內(nèi)有大小相同的1個紅球和3個黑球,乙盒內(nèi)有大小相同的2個紅球和4個黑球,現(xiàn)從甲、乙兩個盒內(nèi)各任取2個球.
(Ⅰ)求取出的4個球中恰有1個紅球的概率;
(Ⅱ)設“從甲盒內(nèi)取出的2個球恰有1個為黑球”為事件A;“從乙盒內(nèi)取出的2個球都是黑球”為事件B,求在事件A發(fā)生的條件下,事件B發(fā)生的概率;
(Ⅲ)設ξ為取出的4個球中紅球的個數(shù),求ξ的分布列和數(shù)學期望.
【答案】
分析:(Ⅰ)設“從甲盒內(nèi)取出的2個球均為黑球;從乙盒內(nèi)取出的2個球中,1個是紅球,1個是黑球”為事件C,“從甲盒內(nèi)取出的2個球中,1個是紅球,1個是黑球;從乙盒內(nèi)取出的2個球均為黑球”為事件D.由事件C、D互斥,能求出取出的4個球中恰有1個紅球的概率.
(Ⅱ)先求出P(A),再由P(AB)=P(D),由此利用條件概率公式P(B/A)=
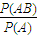
能求出在事件A發(fā)生的條件下,事件B發(fā)生的概率.
(Ⅲ)由題設知ξ可能的取值為0,1,2,3,分別求出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3,由此能求出ξ的分布列的數(shù)學期望.
解答:解:(Ⅰ)設“從甲盒內(nèi)取出的2個球均為黑球;從乙盒內(nèi)取出的2個球中,1個是紅球,1個是黑球”為事件C,“從甲盒內(nèi)取出的2個球中,1個是紅球,1個是黑球;從乙盒內(nèi)取出的2個球均為黑球”為事件D.由于事件C、D互斥,
則P(C)=

=
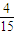
,
P(D)=

=
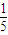
,
∴取出的4個球中恰有1個紅球的概率為
P(C+D)=P(C)+P(D)=
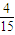
+
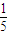
=
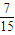
.
(Ⅱ)∵“從甲盒內(nèi)取出的2個球恰有1個為黑球”為事件A,
∴P(A)=

=

,
∵“從乙盒內(nèi)取出的2個球都是黑球”為事件B,
∴P(AB)=P(D)=
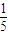
,
∴在事件A發(fā)生的條件下,事件B發(fā)生的概率P(B/A)=
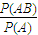
=

=
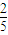
.
(Ⅲ)由題設知ξ可能的取值為0,1,2,3,
由(Ⅰ)、(Ⅱ)得P(ξ=0)=

=

,
P(ξ=1)=
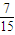
,
P(ξ=3)=

=

,
∴P(ξ=2)=1-P(ξ=0)-P(ξ=1)-P(ξ=3)=

,
∴ξ的分布列為

∴ξ的數(shù)學期望
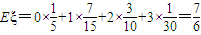
.…(12分)
點評:本題考查離散型隨機變量的分布列與數(shù)學期望的求法,考查條件概率的求法,解題時要認真審題,注意排列組合知識的合理運用.

 能求出在事件A發(fā)生的條件下,事件B發(fā)生的概率.
能求出在事件A發(fā)生的條件下,事件B發(fā)生的概率. =
=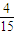 ,
, =
=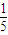 ,
,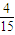 +
+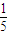 =
=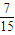 .
. =
= ,
,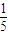 ,
,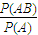 =
= =
=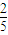 .
. =
= ,
,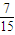 ,
, =
= ,
, ,
,
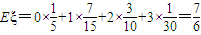 .…(12分)
.…(12分)

 期末沖刺100分創(chuàng)新金卷完全試卷系列答案
期末沖刺100分創(chuàng)新金卷完全試卷系列答案