
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() ,當
,當![]() 時,
時,![]() .數列
.數列![]() 滿足
滿足![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)求數列![]() 的通項公式;
的通項公式;
(3)若數列![]() 的前
的前![]() 項和為
項和為![]() ,求證:
,求證:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)證明見詳解.
;(3)證明見詳解.
【解析】
(1)根據![]() 的關系,即可容易求得
的關系,即可容易求得![]() .
.
(2)由遞推公式,進行下標的縮減,即可求得![]() ;
;
(3)利用等差數列和等比數列的前![]() 項和公式,求得
項和公式,求得![]() ,利用導數即可由函數單調性,進行證明.
,利用導數即可由函數單調性,進行證明.
(1)因為![]() ,
,
故當![]() 時,
時,![]() ,
,
故可得![]() ;
;
又因為![]() ,
,![]() ,解得
,解得![]() .
.
故數列![]() 是首項為
是首項為![]() ,公比為
,公比為![]() 的等比數列,
的等比數列,
則![]() .
.
(2)因為![]() ,①
,①
故可得當![]() 時,
時,![]()
兩邊同乘以![]() ,
,
則![]() ②
②
①![]() ②可得:
②可得:![]() ,則
,則![]() .
.
又當![]() 時,
時,![]() ,故可得
,故可得![]() ,
,
故![]() .
.
(3)由(1)可知,數列![]() 是首項為
是首項為![]() ,公比為
,公比為![]() 的等比數列,
的等比數列,
故可得![]() ;
;
又因為![]() ,故數列
,故數列![]() 是首項為1,公差為
是首項為1,公差為![]() 的等差數列,
的等差數列,
故可得![]() ,
,
又![]() .
.
令![]() ,
,![]() ,
,
因![]() 為單調增函數,且
為單調增函數,且![]() ,
,
故存在![]() ,使得
,使得![]() ,
,
故當![]() 時
時![]() 單調遞減,當
單調遞減,當![]() 時
時![]() 單調遞增.
單調遞增.
又因為![]() ,
,
故存在![]() ,使得
,使得![]() ,
,
故當![]() 時
時![]() 單調遞減,當
單調遞減,當![]() 時
時![]() 單調遞增.
單調遞增.
又因為![]() ,
,
故可得![]() ,當
,當![]() 時
時![]() ,
,
故當![]() 時,
時,![]() ,
,
即![]() .
.
故![]() ,即證.
,即證.


科目:高中數學 來源: 題型:
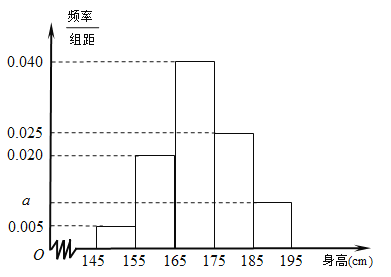
【題目】某中學隨機選取了![]() 名男生,將他們的身高作為樣本進行統計,得到如圖所示的頻率分布直方圖.觀察圖中數據,完成下列問題.
名男生,將他們的身高作為樣本進行統計,得到如圖所示的頻率分布直方圖.觀察圖中數據,完成下列問題.
(Ⅰ)求![]() 的值及樣本中男生身高在
的值及樣本中男生身高在![]() (單位:
(單位: ![]() )的人數;
)的人數;
(Ⅱ)假設同一組中的每個數據可用該組區間的中點值代替,通過樣本估計該校全體男生的平均身高;
(Ⅲ)在樣本中,從身高在![]() 和
和![]() (單位:
(單位: ![]() )內的男生中任選兩人,求這兩人的身高都不低于
)內的男生中任選兩人,求這兩人的身高都不低于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() ,總存在實數
,總存在實數![]() ,使
,使![]() 成立,則稱
成立,則稱![]() 為
為![]() 關于參數
關于參數![]() 的不動點.
的不動點.
(1)當![]() ,
,![]() 時,求
時,求![]() 關于參數
關于參數![]() 的不動點;
的不動點;
(2)若對任意實數![]() ,函數
,函數![]() 恒有關于參數
恒有關于參數![]() 兩個不動點,求
兩個不動點,求![]() 的取值范圍;
的取值范圍;
(3)當![]() ,
,![]() 時,函數
時,函數![]() 在
在![]() 上存在兩個關于參數
上存在兩個關于參數![]() 的不動點,試求參數
的不動點,試求參數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一款擊鼓小游戲的規則如下:每盤游戲都需要擊鼓三次,每次擊鼓要么出現一次音樂,要么不出現音樂;每盤游戲擊鼓三次后,出現一次音樂獲得10分,出現兩次音樂獲得20分,出現三次音樂獲得100分,沒有出現音樂則扣除200分(即獲得![]() 分).設每次擊鼓出現音樂的概率為
分).設每次擊鼓出現音樂的概率為![]() ,且各次擊鼓出現音樂相互獨立.
,且各次擊鼓出現音樂相互獨立.
(1)設每盤游戲獲得的分數為![]() ,求
,求![]() 的分布列;
的分布列;
(2)玩三盤游戲,至少有一盤出現音樂的概率是多少?
(3)玩過這款游戲的許多人都發現,若干盤游戲后,與最初的分數相比,分數沒有增加反而減少了.請運用概率統計的相關知識分析分數減少的原因.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究性學習小組對春季晝夜溫差大小與某花卉種子發芽多少之間的關系進行研究,他們分別記錄了3月1日至3月5日的每天晝夜溫差與實驗室每天每100顆種子浸泡后的發芽數,得到如下資料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
溫差 | 10 | 11 | 13 | 12 | 9 |
發芽數 | 23 | 25 | 30 | 26 | 16 |
(1)從3月1日至3月5日中任選2天,記發芽的種子數分別為![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率;
”的概率;
(2)該小組發現種子的發芽數![]() (顆)與晝夜溫差
(顆)與晝夜溫差![]() (℃)呈線性相關關系,試求:線性回歸方程
(℃)呈線性相關關系,試求:線性回歸方程![]() .
.
(參考公式:線性回歸方程![]() 中系數計算公式
中系數計算公式 ,
,![]() .其中
.其中![]() ,
,![]() 表示樣本均值.
表示樣本均值.
參考數據:![]() ;
;![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著手機的普及,大學生迷戀手機的現象非常嚴重.為了調查雙休日大學生使用手機的時間,某機構采用不記名方式隨機調查了使用手機時間不超過10小時的50名大學生,將50人使用手機的時間分成5組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別加以統計,得到下表,根據數據完成下列問題:
分別加以統計,得到下表,根據數據完成下列問題:
使用時間/時 |
|
|
|
|
|
大學生/人 | 5 | 10 | 15 | 12 | 8 |

(1)完成頻率分布直方圖,并根據頻率分布直方圖估計大學生使用手機時間的中位數(保留小數點后兩位);
(2)用分層抽樣的方法從使用手機時間在區間![]() ,
,![]() ,
,![]() 的大學生中抽取6人,再從這6人中隨機抽取2人,求這2人取自不同使用時間區間的概率.
的大學生中抽取6人,再從這6人中隨機抽取2人,求這2人取自不同使用時間區間的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某射擊運動員每次擊中目標的概率都是![]() ,現采用隨機模擬的方法估計該運動員射擊
,現采用隨機模擬的方法估計該運動員射擊![]() 次至多擊中
次至多擊中![]() 次的概率:先由計算器產生
次的概率:先由計算器產生![]() 到
到![]() 之間取整數值的隨機數,指定
之間取整數值的隨機數,指定![]() 、
、![]() 表示沒有擊中目標,
表示沒有擊中目標,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 表示擊中目標,因為射擊
表示擊中目標,因為射擊![]() 次,故以每
次,故以每![]() 個隨機數為一組,代表射擊
個隨機數為一組,代表射擊![]() 次的結果.經隨機模擬產生了如下
次的結果.經隨機模擬產生了如下![]() 組隨機數:
組隨機數:
5727 0293 7140 9857 0347 4373 8636 9647 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 6710 4281
據此估計,射擊運動員射擊4次至多擊中3次的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《朗讀者》是一檔文化情感類節目,以個人成長、情感體驗、背景故事與傳世佳作相結合的方式,選用精美的文字,用最平實的情感讀出文字背后的價值,深受人們的喜愛.為了了解人們對該節目的喜愛程度,某調查機構隨機調查了![]() ,
,![]() 兩個城市各100名觀眾,得到下面的列聯表.
兩個城市各100名觀眾,得到下面的列聯表.
非常喜愛 | 喜愛 | 合計 | |
| 60 | 100 | |
| 30 | ||
合計 | 200 |
完成上表,并根據以上數據,判斷是否有![]() 的把握認為觀眾的喜愛程度與所處的城市有關?
的把握認為觀眾的喜愛程度與所處的城市有關?
附參考公式和數據: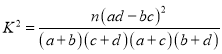 (其中
(其中![]() ).
).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com