【題目】某服裝店對過去100天實體店和網店的銷售量（單位：件）進行了統計，制成頻率分布直方圖如下：
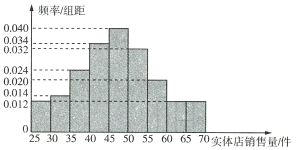
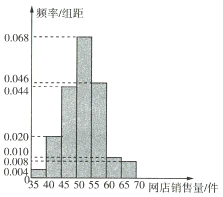
（1）已知該服裝店過去100天的銷售中，實體店和網店的銷售量都不低于50件的頻率為0.24，求過去100天的銷售中，實體店和網店至少有一邊銷售量不低于50件的天數；
（2）根據頻率分布直方圖，求該服裝店網店銷售量的中位數的估計值（精確到0.01）.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】某市為創建全國衛生城市，引入某公司的智能垃圾處理設備.已知每臺設備每月固定維護成本
萬元，每處理一萬噸垃圾需增加
萬元維護費用，每月處理垃圾帶來的總收益
萬元與每月垃圾處理量
（萬噸）滿足關系：
（注：總收益=總成本+利潤）
（1）寫出每臺設備每月處理垃圾獲得的利潤
關于每月垃圾處理量的函數關系；
（2）該市計劃引入
臺這種設備，當每臺每月垃圾處理量為何值時，所獲利潤最大？并求出最大利潤.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知三棱錐P﹣ABC中，AC⊥BC，AC＝BC＝2，PA＝PB＝PC＝3，O是AB中點，E是PB中點．
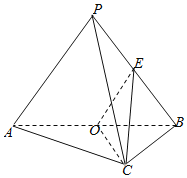
（1）證明：平面PAB⊥平面ABC；
（2）求點B到平面OEC的距離．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了鼓勵市民節約用電，某市實行“階梯式”電價，將每戶居民的月用電量分為二檔，月用電量不超過200度的部分按0.5元/度收費，超過200度的部分按0.8元/度收費.某小區共有居民1000戶，為了解居民的用電情況，通過抽樣，獲得了今年7月份100戶居民每戶的用電量，統計分析后得到如圖所示的頻率分布直方圖.
（1）求
的值；
（2）試估計該小區今年7月份用電量用不超過260元的戶數；
（3）估計7月份該市居民用戶的平均用電費用（同一組中的數據用該組區間的中點值作代表）.
查看答案和解析>>
科目：高中數學 來源： 題型：
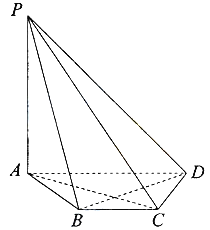
【題目】如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，底面ABCD是等腰梯形，AD∥BC，AC⊥BD.
（Ⅰ）證明：BD⊥PC；
（Ⅱ）若AD=4，BC=2，直線PD與平面PAC所成的角為30°，求四棱錐P-ABCD的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，其中
為自然對數的底數.
（1）若函數
在區間
上是單調函數，試求實數
的取值范圍；
（2）已知函數
，且
，若函數
在區間
上恰有3個零點，求實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線方程為
，其中
（1）求證：直線恒過定點；
（2）當
變化時，求點
到直線的距離的最大值；
（3）若直線分別與
軸、
軸的負半軸交于
兩點，求
面積的最小值及此時的直線方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
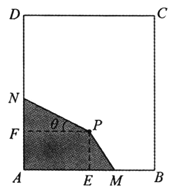
【題目】（題文）如圖，長方形材料
中，已知
，
.點
為材料內部一點，
于
，
于
，且
，
. 現要在長方形材料中裁剪出四邊形材料
，滿足
，點
、
分別在邊
，
上.
（1）設
，試將四邊形材料的面積表示為
的函數，并指明的取值范圍；
（2）試確定點在上的位置，使得四邊形材料的面積
最小，并求出其最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在人群流量較大的街道，有一中年人吆喝“送錢”，只見他手拿一黑色小布袋，袋中有3只黃色、3只白色的乒乓球（其體積、質地完成相同），旁邊立著一塊小黑板寫道：
摸球方法：從袋中隨機摸出3個球，若摸得同一顏色的3個球，攤主送給摸球者5元錢；若摸得非同一顏色的3個球，摸球者付給攤主1元錢．
（1）摸出的3個球為白球的概率是多少？
（2）摸出的3個球為2個黃球1個白球的概率是多少？
（3）假定一天中有100人次摸獎，試從概率的角度估算一下這個攤主一個月（按30天計）能賺多少錢？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
