
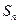 為數(shù)列
為數(shù)列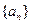 的前
的前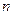 項和,
項和,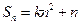 ,
,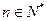 ,其中
,其中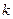 是常數(shù).
是常數(shù).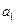 及
及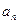 ;
;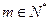 ,
,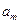 ,
,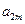 ,
,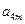 成等比數(shù)列,求
成等比數(shù)列,求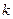 的值.
的值.科目:高中數(shù)學 來源:不詳 題型:解答題
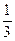 )是函數(shù)
)是函數(shù)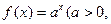 且
且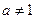 )的圖象上一點,等比數(shù)列
)的圖象上一點,等比數(shù)列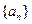 的前
的前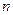 項和為
項和為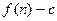 ,數(shù)列
,數(shù)列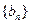
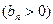 的首項為
的首項為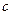 ,且前
,且前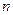 項和
項和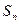 滿足
滿足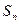 -
-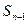 =
=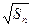 +
+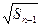 (
(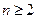 ).
).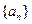 和
和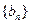 的通項公式;(2)若數(shù)列{
的通項公式;(2)若數(shù)列{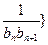 前
前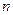 項和為
項和為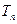 ,問
,問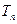 >
>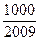 的最小正整數(shù)
的最小正整數(shù)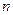 是多少?
是多少? 查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 .
.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 12分)已知等差數(shù)列{an2
12分)已知等差數(shù)列{an2 }中,首項a12=1,公差d=1,an>0,n∈N
}中,首項a12=1,公差d=1,an>0,n∈N *.
*.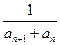 ,數(shù)列{bn}的前120項和T120;
,數(shù)列{bn}的前120項和T120; 查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
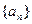 的各項均為正數(shù),
的各項均為正數(shù),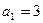 ,前
,前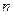 項和為
項和為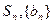 為等比數(shù)列,公比
為等比數(shù)列,公比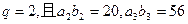 ;
;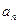 與
與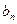 ;
; 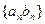 的前
的前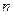 項和
項和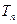 ;
;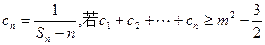 對任意正整數(shù)
對任意正整數(shù)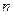 恒成立,求實數(shù)
恒成立,求實數(shù)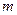 的取值范圍。
的取值范圍。查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
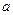 萬元,年利率為
萬元,年利率為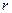 ,按復利計算,從2010年末開始,每年末償還一定金額,計劃第5年底還清,則每年應償還的金額數(shù)為( )萬元.
,按復利計算,從2010年末開始,每年末償還一定金額,計劃第5年底還清,則每年應償還的金額數(shù)為( )萬元.A. | B.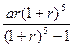 | C.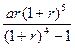 | D.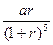 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
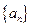 滿足:
滿足: 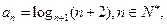 我們把使
我們把使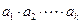 為整數(shù)的數(shù)
為整數(shù)的數(shù)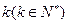 叫做數(shù)列
叫做數(shù)列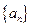 的理想數(shù),給出下列關于數(shù)列
的理想數(shù),給出下列關于數(shù)列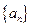 的幾個結論:
的幾個結論: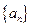 的最小理想數(shù)是2; ②數(shù)列
的最小理想數(shù)是2; ②數(shù)列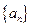 的理想數(shù)k的形式可以表示為
的理想數(shù)k的形式可以表示為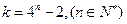
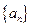 的所有理想數(shù)之和為1004; ④對任意
的所有理想數(shù)之和為1004; ④對任意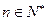 ,有
,有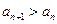 ,
,| A.3 | B.2 | C.1 | D.0 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
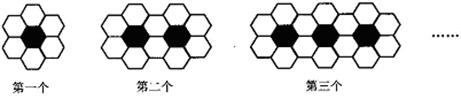
A.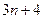 | B.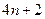 | C.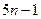 | D.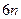 |
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com