(本小題滿分12分)
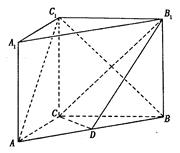
如圖, 在直三棱柱ABC-A
1B
1C
1中,AC=3,BC=4,
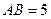
,AA
1=3,點D是AB的中點.
(Ⅰ)求證:
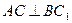
(Ⅱ)求二面角
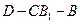
的大小.
解:(本小題滿分12分)
(Ⅰ)直三棱柱ABC-A
1B
1C
1,底面三邊長AC=3,BC=4,AB=5,
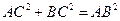
,∴ AC⊥BC,………………………2分
又 AC⊥
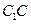
,且
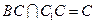
,
∴ AC⊥平面BCC
1,又
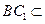
平面BCC
1 , …………………………………4分
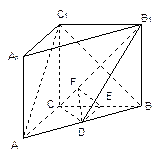
∴ AC⊥BC
1 .…………………………………………………………5分
(Ⅱ)取
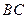
中點
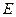
,過
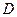
作
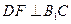
于
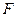
,連接
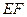
.
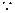
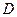
是
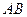
中點,∴
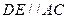
.
又
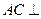
平面
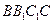
,∴
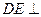
平面
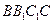
.
又
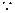
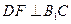
,∴
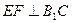
.
∴
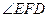
是二面角
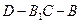
的平面角.…………………………………………………8分
在
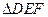
中,求得
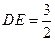
,
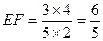
.
∴
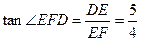
.
∴二面角
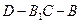
的大小為
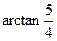
. …………………………………………12分
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
、如圖,四棱錐S—ABCD的底面是邊長為1的正方形,SD垂直于底面ABCD,SD=1,SB=

.

(I)求證BC

SC; (II)求平

面SBC與平面ABCD所成二面角的大小;
(III)設(shè)棱SA的中點為M,求異面直線DM與SB所成角的大小
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
、(本題12分)在正方體
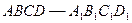
中

,

求證:(1)對角線
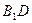
⊥平面
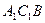
。
(2)
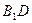
與平面
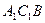
的交點H是
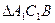
的外心。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
如圖,在四棱錐P—ABCD中,底面ABCD是正方形,PA⊥平面ABCD,且PA=AB=2,E、F分別為AB、PC的中點。
(1)求異面直線PA與BF所成角的正切值。
(2)

求證:EF⊥平面PCD。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
((本小題滿分12分)
若圖為一簡單組合體,其底面ABCD為正方形,PD
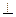
平面ABCD,EC//PD,且PD=2EC。
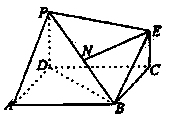
(1)求證:BE//平面PDA;
(2)若N為線段PB的中點,求證:EN
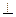
平面PDB;
(3)若
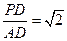
,求平面PBE與平面ABCD所成的二面角的大小。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(16分)如圖,四棱錐
S-ABCD的底面是正方形,每條側(cè)棱的長都是地面邊長的

倍,
P為側(cè)棱SD上的點。
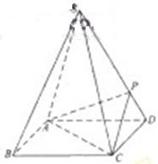
(Ⅰ)求證:
AC⊥
SD;
(Ⅱ)若
SD⊥
平面PAC,求二面角
P-AC-D的大小
(Ⅲ)在(Ⅱ)的條件下,側(cè)棱SC上是否存在一點E,使得BE∥平
面PAC。若存在,求SE:EC的值

;若不存在,試說明理由。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
( (本小題滿分12分)
在棱長為4的正方體ABCD-A1B1C1D1中,O是正方形A1B1C1D1的中心,點P在棱CC1上,且CC1=4CP.

(1)、求直線AP與平面BCC1B1所成的角的大小(結(jié)果用反三角函數(shù)值表示);
(2)、求點P到平面ABD1的距離.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
(文科)已知平面
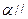
平面
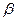
,
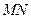
和
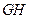
是夾在
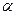
、
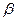
間的兩條線段,
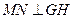
,
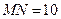
直線
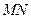
與
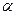
成
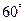
角,則線段
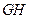
的最小值是 ( )
A.
 B
B.
 C
C.
 D
D.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
((本題滿分13分)
如圖,在三棱柱
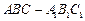
中,
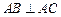
,頂點
在底面
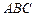
上的射影恰為點
B,且
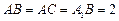
.

(1)求棱
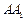
與
BC所成的角的大小;
(2)在線段
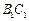
上確定一點
P,使
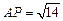
,并求出二面角
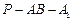
的平面角的余弦值.
查看答案和解析>>

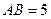 ,AA1=3,點D是AB的中點.
,AA1=3,點D是AB的中點.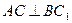
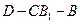 的大小.
的大小.
 .
.
 SC; (II)求平
SC; (II)求平 面SBC與平面ABCD所成二面角的大小;
面SBC與平面ABCD所成二面角的大小; 求證:EF⊥平面PCD。
求證:EF⊥平面PCD。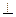 平面ABCD,EC//PD,且PD=2EC。
平面ABCD,EC//PD,且PD=2EC。
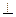 平面PDB;
平面PDB;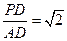 ,求平面PBE與平面ABCD所成的二面角的大小。
,求平面PBE與平面ABCD所成的二面角的大小。 倍,
倍,
 ;若不存在,試說明理由。
;若不存在,試說明理由。
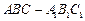 中,
中,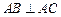 ,頂點
,頂點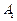 在底面
在底面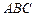 上的射影恰為點B,且
上的射影恰為點B,且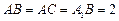 .
.
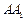 與BC所成的角的大小;
與BC所成的角的大小;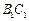 上確定一點P,使
上確定一點P,使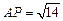 ,并求出二面角
,并求出二面角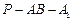 的平面角的余弦值.
的平面角的余弦值.