
【題目】如圖,在四棱錐![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
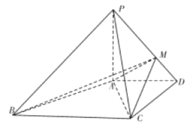
(1)取![]() 中點
中點![]() ,求證:
,求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與
與![]() 所成角的余弦值.
所成角的余弦值.
(3)在線段![]() 上,是否存在一點
上,是否存在一點![]() ,使得二面角
,使得二面角![]() 的大小為
的大小為![]() ,如果存在,求
,如果存在,求![]() 與平面
與平面![]() 所成角,如果不存在,請說明理由.
所成角,如果不存在,請說明理由.
【答案】(1)見解析(2) ![]() (3)見解析
(3)見解析
【解析】
試題分析:(1)建立如圖所示的坐標系,先求![]() 的方向向量,再出利用向量垂直數(shù)量積為零,列方程組求出平面
的方向向量,再出利用向量垂直數(shù)量積為零,列方程組求出平面![]() 的法向量
的法向量![]() ,由
,由![]() 可得結果;(2)分別求出直線
可得結果;(2)分別求出直線![]() 與
與![]() 的方向向量,利用空間向量夾角余弦公式可得直線
的方向向量,利用空間向量夾角余弦公式可得直線![]() 與
與![]() 所成角的余弦值(結果注意取絕對值);(3)
所成角的余弦值(結果注意取絕對值);(3)![]() ,
,![]() ,分別根據(jù)向量垂直數(shù)量積為零列方程組求出平面
,分別根據(jù)向量垂直數(shù)量積為零列方程組求出平面![]() 與平面
與平面![]() 的一個法向量,根據(jù)空間向量夾角余弦公式,可得
的一個法向量,根據(jù)空間向量夾角余弦公式,可得![]() ,從而可確定
,從而可確定![]() 的坐標,利用
的坐標,利用![]() 可得結果.
可得結果.
試題解析:如圖建系:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
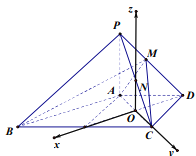
(1)![]() 中點
中點![]() ,
,
∴![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,由
,由![]() ,
,![]() ,
,
可得:![]() ,∴
,∴![]() ,∵
,∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)![]() ,
,![]() ,
,
∴![]() .
.
(3)設![]() 及
及![]() ,
,
∴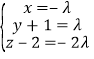
![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
由![]() ,
,![]() 可得
可得![]() ,
,
平面![]() 的法向量為
的法向量為![]() ,
,
∴![]()
![]() ,
,
解得![]() .
.
∴![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]()
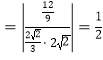 ,∴
,∴![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】(本小題滿分12分)
已知函數(shù)![]() (其中a是實數(shù)).
(其中a是實數(shù)).
(1)求![]() 的單調區(qū)間;
的單調區(qū)間;
(2)若設![]() ,且
,且![]() 有兩個極值點
有兩個極值點![]()
![]() ,求
,求![]() 取值范圍.(其中e為自然對數(shù)的底數(shù)).
取值范圍.(其中e為自然對數(shù)的底數(shù)).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】給定函數(shù)![]() 和
和![]() ,若存在常數(shù)
,若存在常數(shù)![]() ,
,![]() ,使得函數(shù)
,使得函數(shù)![]() 和
和![]() 對其公共定義域
對其公共定義域![]() 的任何實數(shù)
的任何實數(shù)![]() 分別滿足
分別滿足![]() 和
和![]() ,則稱直線
,則稱直線![]() :
:![]() 為函數(shù)
為函數(shù)![]() 和
和![]() 的“隔離直線”,給出下列四組函數(shù):
的“隔離直線”,給出下列四組函數(shù):
(1)![]() ,
,![]() ; (2)
; (2)![]() ,
,![]() ;
;
(3)![]() ,
,![]() ; (4)
; (4)![]() ,
,![]() ;
;
其中函數(shù)![]() 和
和![]() 存在“隔離直線”的序號是( )
存在“隔離直線”的序號是( )
A.(1)(3)B.(1)(3)(4)C.(1)(2)(3)D.(2)(4)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】春節(jié)過后,甲、乙、丙三人談論到有關![]() 部電影
部電影![]() ,
,![]() ,
,![]() 的情況.
的情況.
甲說:我沒有看過電影![]() ,但是有
,但是有![]() 部電影我們三個都看過;
部電影我們三個都看過;
乙說:三部電影中有![]() 部電影我們三人中只有一人看過;
部電影我們三人中只有一人看過;
丙說:我和甲看的電影有![]() 部相同,有
部相同,有![]() 部不同.
部不同.
假如他們都說的是真話,則由此可判斷三部電影中乙看過的部數(shù)是( )
A.![]() 部B.
部B.![]() 部C.
部C.![]() 部D.
部D.![]() 部或
部或![]() 部
部
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了調查某大學學生的某天上網(wǎng)的時間,隨機對![]() 名男生和
名男生和![]() 名女生進行了不記名的問卷調查.得到了如下的統(tǒng)計結果:
名女生進行了不記名的問卷調查.得到了如下的統(tǒng)計結果:
表1:男生上網(wǎng)時間與頻數(shù)分布表
上網(wǎng)時間(分鐘) |
|
|
|
|
|
人數(shù) |
|
|
|
|
|
表2:女生上網(wǎng)時間與頻數(shù)分布表
上網(wǎng)時間(分鐘) |
|
|
|
|
|
人數(shù) |
|
|
|
|
|
(1)用分層抽樣在![]() 選取
選取![]() 人,再隨機抽取
人,再隨機抽取![]() 人,求抽取的
人,求抽取的![]() 人都是女生的概率;
人都是女生的概率;
(2)完成下面的![]() 列聯(lián)表,并回答能否有
列聯(lián)表,并回答能否有![]() 的把握認為“大學生上網(wǎng)時間與性別有關”?
的把握認為“大學生上網(wǎng)時間與性別有關”?
上網(wǎng)時間少于 | 上網(wǎng)時間不少于 | 合計 | |
男生 | |||
女生 | |||
合計 |
附: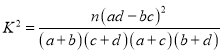
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】三角形的三個頂點的坐標分別為![]() ,
,![]() ,
,![]() ,則該三角形的重心(三邊中線交點)的坐標為
,則該三角形的重心(三邊中線交點)的坐標為![]() .類比這個結論,連接四面體的一個頂點及其對面三角形重心的線段稱為四面體的中線,四面體的四條中線交于一點,該點稱為四面體的重心.若四面體的四個頂點的空間坐標分別為
.類比這個結論,連接四面體的一個頂點及其對面三角形重心的線段稱為四面體的中線,四面體的四條中線交于一點,該點稱為四面體的重心.若四面體的四個頂點的空間坐標分別為![]() ,
,![]() ,
,![]() ,
,![]() ,則該四面體的重心的坐標為( )
,則該四面體的重心的坐標為( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 的圖像過點
的圖像過點![]() ,且在
,且在![]() 處取得極值.
處取得極值.
(1)若對任意![]() 有
有![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)當![]() ,試討論函數(shù)
,試討論函數(shù)![]() 的零點個數(shù).
的零點個數(shù).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】隨著生活節(jié)奏的加快以及智能手機的普及,外賣點餐逐漸成為越來越多用戶的餐飲消費習慣.由此催生了一批外賣點餐平臺,已知某外賣平臺的送餐費用與送餐距離有關(該平臺只給5千米范圍內配送),為調査送餐員的送餐收入,現(xiàn)從該平臺隨機抽取80名點外賣的用戶進行統(tǒng)計,按送餐距離分類統(tǒng)計結果如下表:

以這80名用戶送餐距離位于各區(qū)間的頻率代替送餐距離位于該區(qū)間的概率.
(1)從這80名點外賣的用戶中任取一名用戶.求該用戶的送餐距離不超過3千米的概率;
(2)試估計利用該平臺點外賣用戶的平均送餐距離;
(3)若該外賣平臺給送餐員的送餐贄用與送餐距離有關,規(guī)定2千米內為短距離,每份3元,2千米到4千米為中距離,每份5元;超過4千米為遠距離,每份9元,若送餐員一天的目標收 人不低于150元,試估計一天至少要送多少份外賣?
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com