
(15分)已知函數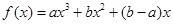 (
(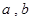 不同時為零的常數),導函數為
不同時為零的常數),導函數為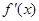 .
.
(Ⅰ)當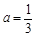 時,若存在
時,若存在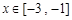 使得
使得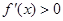 成立,求
成立,求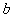 的取值范圍;
的取值范圍;
(Ⅱ)求證:函數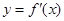 在
在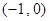 內至少有一個零點;
內至少有一個零點;
(Ⅲ)若函數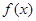 為奇函數,且在
為奇函數,且在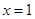 處的切線垂直于直線
處的切線垂直于直線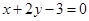 ,關于
,關于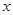 的方程
的方程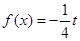 在
在 上有且只有一個實數根,求實數
上有且只有一個實數根,求實數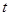 的取值范圍.
的取值范圍.
(1)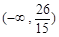 ;(2)函數
;(2)函數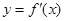 在
在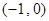 內至少有一個零點;(3)
內至少有一個零點;(3)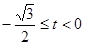 或
或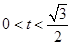 .
.
【解析】第一問利用當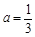 時,
時,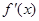 =
=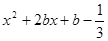 =
=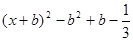 ,其對稱軸為直線
,其對稱軸為直線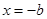 ,
,
當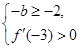 ,解得
,解得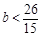 ,當
,當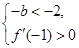
 ,
,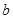 無解,
無解,
所以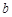 的的取值范圍為
的的取值范圍為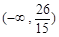
第二問中,法二: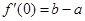 ,
,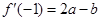 ,
,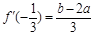 .
.
由于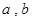 不同時為零,所以
不同時為零,所以 ,故結論成立.
,故結論成立.
第三問中,)因為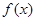 =
=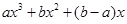 為奇函數,所以
為奇函數,所以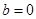 , 所以
, 所以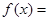
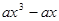 ,
,
又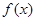 在
在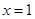 處的切線垂直于直線
處的切線垂直于直線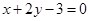 ,所以
,所以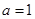 ,即
,即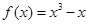 .
.
因為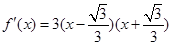 所以
所以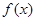 在
在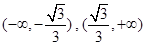 上是増函數,在
上是増函數,在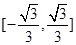 上是減函數,由
上是減函數,由 解得
解得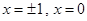 ,結合圖像和極值點得到結論。
,結合圖像和極值點得到結論。
解:(1)當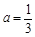 時,
時,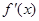 =
=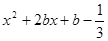 =
=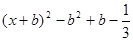 ,其對稱軸為直線
,其對稱軸為直線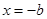 ,
,
當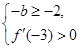 ,解得
,解得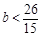 ,當
,當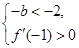
 ,
,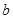 無解,
無解,
所以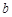 的的取值范圍為
的的取值范圍為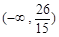 .………………………………………………4分
.………………………………………………4分
(2)因為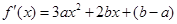 ,
,
法一:當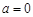 時,
時,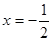 適合題意………………………………………6分
適合題意………………………………………6分
當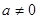 時,
時,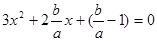 ,令
,令 ,則
,則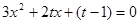 ,
,
令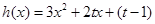 ,因為
,因為 ,
,
當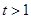 時,
時,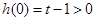 ,所以
,所以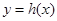 在
在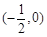 內有零點.
內有零點.
當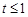 時,
時,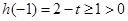 ,所以
,所以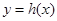 在(
在(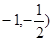 內有零點.
內有零點.
因此,當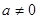 時,
時,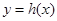 在
在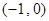 內至少有一個零點.
內至少有一個零點.
綜上可知,函數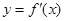 在
在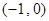 內至少有一個零點.……………………10分
內至少有一個零點.……………………10分
法二: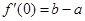 ,
,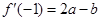 ,
,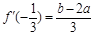 .
.
由于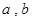 不同時為零,所以
不同時為零,所以 ,故結論成立.
,故結論成立.
(3)因為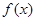 =
=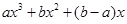 為奇函數,所以
為奇函數,所以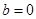 , 所以
, 所以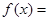
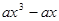 ,
,
又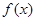 在
在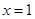 處的切線垂直于直線
處的切線垂直于直線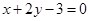 ,所以
,所以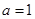 ,即
,即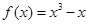 .
.
因為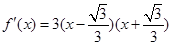 所以
所以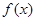 在
在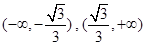 上是増函數,在
上是増函數,在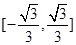 上是減函數,由
上是減函數,由 解得
解得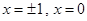 ,如圖所示,
,如圖所示,
 當
當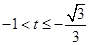 時,
時,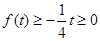 ,即
,即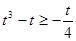 ,解得
,解得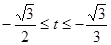 ;
;
當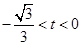 時,
時,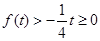 ,解得
,解得 ;
;
當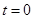 時,顯然不成立;
時,顯然不成立;
當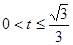 時,
時,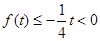 ,即
,即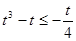 ,
,
解得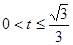 ;
;
當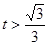 時,
時,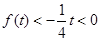 ,故
,故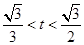 .
.
所以所求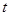 的取值范圍是
的取值范圍是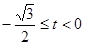 或
或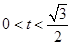 .
.


 智能訓練練測考系列答案
智能訓練練測考系列答案 計算高手系列答案
計算高手系列答案科目:高中數學 來源: 題型:
| a |
| ||
| 2 |
| 1 |
| 2 |
| b |
| 1 |
| 2 |
| ||
| 2 |
| a |
| b |
| x |
| a |
| b |
| y |
| a |
| b |
| x |
| y |
查看答案和解析>>
科目:高中數學 來源:江蘇省期中題 題型:解答題
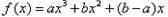 (
(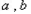 不同時為零的常數),導函數為
不同時為零的常數),導函數為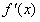
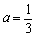 時,若存在
時,若存在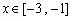 ,使得
,使得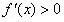 成立,求
成立,求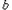 的取值范圍;
的取值范圍;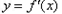 在
在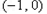 內至少有一個零點;
內至少有一個零點; 為奇函數,且在
為奇函數,且在 處的切線垂直于直線
處的切線垂直于直線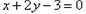 ,關于
,關于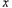 的方程
的方程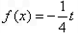 在
在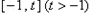 上有且只有一個實數根,求實數
上有且只有一個實數根,求實數 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分16分)
已知函數![]() 是不同時為零的常數),其導函數為
是不同時為零的常數),其導函數為![]() 。
。
當a=![]() 時,若存在
時,若存在![]() ,使得
,使得![]() >成立,求b的取值范圍;
>成立,求b的取值范圍;
求證:函數y=![]() d (-1,0)內至少存在一個零點;
d (-1,0)內至少存在一個零點;
若函數f(x)為奇函數,且在x=1處的切線垂直于在線x+2y-3=0, 關于x的方程![]() 在[-1,t](t>-1)上有且只有一個實數根,求實數t的取值范圍。
在[-1,t](t>-1)上有且只有一個實數根,求實數t的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
(本題滿分16分)
已知函數![]() 是不同時為零的常數),其導函數為
是不同時為零的常數),其導函數為![]() 。
。
當a=![]() 時,若存在
時,若存在![]() ,使得
,使得![]() >成立,求b的取值范圍;
>成立,求b的取值范圍;
求證:函數y=![]() d (-1,0)內至少存在一個零點;
d (-1,0)內至少存在一個零點;
若函數f(x)為奇函數,且在x=1處的切線垂直于在線x+2y-3=0, 關于x的方程![]() 在[-1,t](t>-1)上有且只有一個實數根,求實數t的取值范圍。
在[-1,t](t>-1)上有且只有一個實數根,求實數t的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com