
【題目】已知極坐標系的極點與直角坐標系的原點重合,極軸與x軸的非負半軸重合.曲線 ![]() (t為參數),曲線C2的極坐標方程為ρ=ρcos2θ+8cosθ. (Ⅰ)將曲線C1 , C2分別化為普通方程、直角坐標方程,并說明表示什么曲線;
(t為參數),曲線C2的極坐標方程為ρ=ρcos2θ+8cosθ. (Ⅰ)將曲線C1 , C2分別化為普通方程、直角坐標方程,并說明表示什么曲線;
(Ⅱ)設F(1,0),曲線C1與曲線C2相交于不同的兩點A,B,求|AF|+|BF|的值.
【答案】解:(Ⅰ)曲線 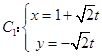 (t為參數),
(t為參數),
將曲線C1的參數方程消去參數t,
化為普通方程得y=﹣x+1,表示一條直線.
曲線C2的極坐標方程為ρ=ρcos2θ+8cosθ.
由cos2θ=1﹣2sin2θ,得曲線C2的方程可變形為ρ2sin2θ=4ρcosθ,
化為直角坐標方程可得y2=4x,曲線C2表示頂點在原點,焦點為(1,0)的拋物線
(Ⅱ)由 ![]() ,消去y,可得x2﹣6x+1=0
,消去y,可得x2﹣6x+1=0
設A(x1,y1),B(x2,y2),則x1+x2=6,
由題意知F(1,0)為曲線C2的焦點
所以|AF|+|BF|=(x1+1)+(x2+1)=x1+x2+2=8
【解析】(Ⅰ)曲線C1的參數方程消去參數t,化為普通方程得y=﹣x+1,表示一條直線;由cos2θ=1﹣2sin2θ,得曲線C2的方程可變形為ρ2sin2θ=4ρcosθ,化為直角坐標方程可得y2=4x,曲線C2表示頂點在原點,焦點為(1,0)的拋物線.(Ⅱ)由 ![]() ,得x2﹣6x+1=0,由題意知F(1,0)為曲線C2的焦點,由此能求出|AF|+|BF|的值.
,得x2﹣6x+1=0,由題意知F(1,0)為曲線C2的焦點,由此能求出|AF|+|BF|的值.


科目:高中數學 來源: 題型:
【題目】已知函數h(x)=(m2﹣5m+1)xm+1為冪函數,且為奇函數.
(1)求m的值;
(2)求函數g(x)=h(x)+ ![]() 在x∈[0,
在x∈[0, ![]() ]的值域.
]的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某社區居民的家庭年收入與年支出的關系,隨機調查了該社區5戶家庭,得到如下統計數據表:
收入x(萬元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y(萬元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
根據上表可得回歸直線方程 ![]() ,其中
,其中 ![]() ,
, ![]() =
= ![]() ﹣
﹣ ![]() ,據此估計,該社區一戶居民年收入為15萬元家庭的年支出為萬元.
,據此估計,該社區一戶居民年收入為15萬元家庭的年支出為萬元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中華人民共和國個人所得稅法》規定,公民全月工資、薪金(扣除三險一金后)所得不超過3500元的部分不必納稅,超過3500元的部分為全月應納稅所得額個人所得稅計算公式:應納稅額=工資-三險一金=起征點. 其中,三險一金標準是養老保險8%、醫療保險2%、失業保險1%、住房公積金8%,此項稅款按下表分段累計計算:
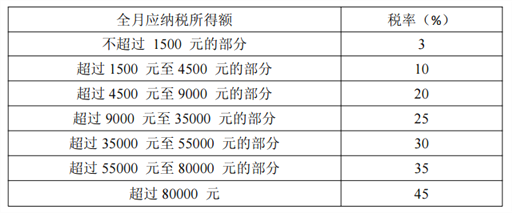
(1)某人月收入15000元(未扣三險一金),他應交個人所得稅多少元?
(2)某人一月份已交此項稅款為1094元,那么他當月的工資(未扣三險一金)所得是多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】閱讀與探究
人教A版《普通高中課程標準實驗教科書 數學4(必修)》在第一章的小結中寫到:
將角放在直角坐標系中討論不但使角的表示有了統一的方法,而且使我們能夠借助直角坐標系中的單位圓,建立角的變化與單位圓上點的變化之間的對應關系,從而用單位圓上點的縱坐標、橫坐標來表示圓心角的正弦函數、余弦函數.因此,正弦函數、余弦函數的基本性質與圓的幾何性質(主要是對稱性)之間存在著非常緊密的聯系.例如,和單位圓相關的“勾股定理”與同角三角函數的基本關系有內在的一致性;單位圓周長為![]() 與正弦函數、余弦函數的周期為
與正弦函數、余弦函數的周期為![]() 是一致的;圓的各種對稱性與三角函數的奇偶性、誘導公式等也是一致的等等.因此,三角函數的研究過程能夠很好地體現數形結合思想.
是一致的;圓的各種對稱性與三角函數的奇偶性、誘導公式等也是一致的等等.因此,三角函數的研究過程能夠很好地體現數形結合思想.

依據上述材料,利用正切線可以討論研究得出正切函數![]() 的性質.
的性質.
比如:由圖1.2-7可知,角![]() 的終邊落在四個象限時均存在正切線;角
的終邊落在四個象限時均存在正切線;角![]() 的終邊落在
的終邊落在![]() 軸上時,其正切線縮為一個點,值為
軸上時,其正切線縮為一個點,值為![]() ;角
;角![]() 的終邊落在
的終邊落在![]() 軸上時,其正切線不存在;所以正切函數
軸上時,其正切線不存在;所以正切函數![]() 的定義域是
的定義域是![]() .
.
(1)請利用單位圓中的正切線研究得出正切函數![]() 的單調性和奇偶性;
的單調性和奇偶性;
(2)根據閱讀材料中途1.2-7,若角![]() 為銳角,求證:
為銳角,求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在正方體ABCD﹣A1B1C1D1中,E、F分別是棱DD1、C1D1的中點. 
(Ⅰ)證明:平面ADC1B1⊥平面A1BE;
(Ⅱ)證明:B1F∥平面A1BE;
(Ⅲ)若正方體棱長為1,求四面體A1﹣B1BE的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com