
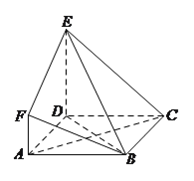
【題目】如圖,在四棱錐A﹣BCFE中,四邊形EFCB為梯形,EF∥BC,且EF= ![]() BC,△ABC是邊長為2的正三角形,頂點F在AC上的射影為點G,且FG=
BC,△ABC是邊長為2的正三角形,頂點F在AC上的射影為點G,且FG= ![]() ,CF=
,CF= ![]() ,BF=
,BF= ![]() .
. 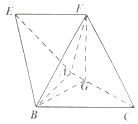
(1)證明:平面FGB⊥平面ABC;
(2)求二面角E﹣AB﹣F的余弦值.
【答案】
(1)證明:由頂點F在AC上投影為點G,可知,FG⊥AC.
取AC的中點為O,連結OB,GB.
在Rt△FGC中, ![]() ,
, ![]() ,所以
,所以 ![]() .
.
在Rt△GBO中, ![]() ,
, ![]() ,所以
,所以 ![]() .
.
所以,BG2+GF2=FB2,即FG⊥BG.
∵FG⊥AC,FG⊥GB,AC∩BG=G
∴FG⊥面ABC.
又FG面FGB,所以面FGB⊥面ABC
(2)解:由(Ⅰ)知,OB⊥FG,OB⊥AC,且AC∩FG=G
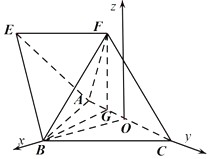
所以 OB⊥面AFC,且FG⊥面ABC.以OB所在直線為x軸,OC所在直線為y軸,
過點O作平面ABC的垂線為z軸,建立空間直角坐標系,如圖所示:
![]() ,
, ![]() ,
,
![]() ,
, ![]() =(0,﹣
=(0,﹣ ![]() ,
, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ),
),
設平面ABE,ABF的法向量分別為 ![]() ,
, ![]() ,
,
則 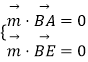 ,即
,即 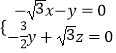 ,取x=1,得
,取x=1,得 ![]() =(1,﹣
=(1,﹣ ![]() ,﹣
,﹣ ![]() ),
),
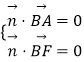 ,即
,即 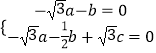 ,取a=1,得
,取a=1,得 ![]() ,
,
設二面角E﹣AB﹣F的平面角為θ.
則cosθ= 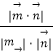 =
= ![]() =
= ![]() .
.
所以二面角E﹣AB﹣F的余弦值為 ![]() .
.
【解析】(1)推導出FG⊥AC,取AC的中點為O,連結OB,GB,推導出FG⊥BG,FG⊥AC,從而FG⊥面ABC,由此能證明面FGB⊥面ABC.(2)以OB所在直線為x軸,OC所在直線為y軸,過點O作平面ABC的垂線為z軸,建立空間直角坐標系,利用向量法能求出二面角E﹣AB﹣F的余弦值.
【考點精析】根據題目的已知條件,利用平面與平面垂直的判定的相關知識可以得到問題的答案,需要掌握一個平面過另一個平面的垂線,則這兩個平面垂直.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]()
(1)求證:直線![]() 過定點;
過定點;
(2)求直線![]() 被圓
被圓![]() 所截得的弦長最短時
所截得的弦長最短時![]() 的值;
的值;
(3)已知點![]() ,在直線MC上(C為圓心),存在定點N(異于點M),滿足:對于圓C上任一點P,都有
,在直線MC上(C為圓心),存在定點N(異于點M),滿足:對于圓C上任一點P,都有![]() 為一常數,試求所有滿足條件的點N的坐標及該常數.
為一常數,試求所有滿足條件的點N的坐標及該常數.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市為了解游客人數的變化規律,提高旅游服務質量,收集并整理了2014年1月至2016年12月期間月接待游客量(單位:萬人)的數據,繪制了如圖所示的折線圖.

根據該折線圖,下列結論錯誤的是( )
A. 月接待游客量逐月增加
B. 年接待游客量逐年增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相對于7月至12月,波動性更小,變化比較平穩
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2015年我國將加快階梯水價推行,原則是“保基本、建機制、促節約”,其中“保基本”是指保證至少80%的居民用戶用水價格不變.為響應國家政策,制定合理的階梯用水價格,某城市采用簡單隨機抽樣的方法分別從郊區和城區抽取5戶和20戶居民的年人均用水量進行調研,抽取的數據的莖葉圖如下(單位:噸):

(1)在郊區的這5戶居民中隨機抽取2戶,求其年人均用水量都不超過30噸的概率;
(2)設該城市郊區和城區的居民戶數比為![]() ,現將年人均用水量不超過30噸的用戶定義為第一階梯用戶,并保證這一梯次的居民用戶用水價格保持不變.試根據樣本估計總體的思想,分析此方案是否符合國家“保基本”政策.
,現將年人均用水量不超過30噸的用戶定義為第一階梯用戶,并保證這一梯次的居民用戶用水價格保持不變.試根據樣本估計總體的思想,分析此方案是否符合國家“保基本”政策.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 內一點
內一點![]() ,直線
,直線![]() 過點
過點![]() 且與圓
且與圓![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
(1)求圓![]() 的圓心坐標和面積;
的圓心坐標和面積;
(2)若直線![]() 的斜率為
的斜率為![]() ,求弦
,求弦![]() 的長;
的長;
(3)若圓上恰有三點到直線![]() 的距離等于
的距離等于![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了比較注射![]() 兩種藥物后產生的皮膚皰疹的面積,選200只家兔做試驗,將這200只家兔隨機地分成兩組,毎組100只,其中一組注射藥物
兩種藥物后產生的皮膚皰疹的面積,選200只家兔做試驗,將這200只家兔隨機地分成兩組,毎組100只,其中一組注射藥物![]() ,另一組注射藥物
,另一組注射藥物![]() .
.
(1)甲、乙是200只家兔中的2只,求甲、乙分在不同組的概率;
(2)下表1和表2分別是注射藥物![]() 和
和![]() 后的試驗結果.(皰疹面積單位:
后的試驗結果.(皰疹面積單位: ![]() )
)
表1:注射藥物![]() 后皮膚皰疹面積的頻數分布表
后皮膚皰疹面積的頻數分布表

表2:注射藥物![]() 后皮膚皰疹面積的頻數分布表
后皮膚皰疹面積的頻數分布表

(ⅰ)完成下面頻率分布直方圖,并比較注射兩種藥物后皰疹面積的中位數大小;
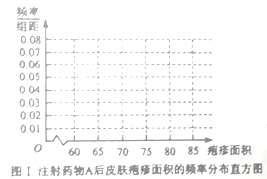
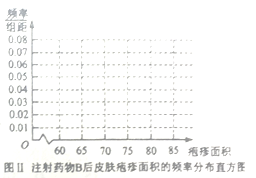
(ⅱ)完成下面![]() 列聯表,并回答能否有
列聯表,并回答能否有![]() 的把握認為“注射藥物
的把握認為“注射藥物![]() 后的皰疹面積與注射藥物
后的皰疹面積與注射藥物![]() 后的皰疹面積有差異”.
后的皰疹面積有差異”.
表3:

附: 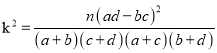
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 是邊長為
是邊長為![]() 的正方形,
的正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 與平面
與平面![]() 所成角為
所成角為![]() .
.
(Ⅰ)求證:![]() 平面
平面![]() .
.
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅲ)設點![]() 是線段
是線段![]() 上一個動點,試確定點
上一個動點,試確定點![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ,并證明你的結論.
,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E: ![]() +
+ ![]() =1(a>b>0)經過點(﹣1,
=1(a>b>0)經過點(﹣1, ![]() ),其離心率e=
),其離心率e= ![]() .
.
(Ⅰ)求橢圓E的方程;
(Ⅱ)設動直線l:y=kx+m與橢圓C相切,切點為T,且l與直線x=﹣4相交于點S.
試問:在x軸上是否存在一定點,使得以ST為直徑的圓恒過該定點?若存在,求出該點的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com