f(x)和g(x)都是定義在集合M上的函數,對于任意的x∈M,都有f(g(x))=g(f(x))成立,稱函數f(x)與g(x)在M上互為“H函數”.
(1)若函數f(x)=ax+b,g(x)=mx+n,f(x)與g(x)互為“H函數”,證明:f(n)=g(b)
(2)若集合M=[-2,2],函數f(x)=x2,g(x)=cosx,判斷函數f(x)與g(x)在M上是否互為“H函數”,并說明理由.
(3)函數f(x)=ax(a>0且a≠1),g(x)=x+1在集合M上互為“H函數”,求a的取值范圍及集合M.
【答案】
分析:(1)由f(x)=ax+b,g(x)=mx+n,f(x)與g(x)互為“H函數”,知f(g(x))=g(f(x))成立.即ag(x)+b=mf(x)+n恒成立,由此能夠證明f(n)=g(b).
(2)假設函數f(x)與g(x)互為“H函數”,則對于任意的x∈M,f(g(x))=g(f(x))恒成立.即cosx
2=cos
2x,對于任意x∈[-2,2]恒成立,由此能推導出在集合M上,函數f(x)與g(x)不是互為“H函數”.
(3)由題意得,a
x+1=a
x+1(a>0且a≠1),變形得a
x(a-1)=1,由于a>0且a≠1
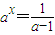
,由此能求出a的取值范圍及集合M.
解答:(1)證明:∵f(x)=ax+b,
g(x)=mx+n,f(x)與g(x)互為“H函數”,
∴對于?x∈R,f(g(x))=g(f(x))成立.
即ag(x)+b=mf(x)+n恒成立…(2分)
∴max+an+b=amx+mb+n,…(2分)
∴an+b=mb+n,
∴f(n)=g(b).…(1分)
(2)解:假設函數f(x)與g(x)互為“H函數”,
則對于任意的x∈Mf(g(x))=g(f(x))恒成立.
即cosx
2=cos
2x,對于任意x∈[-2,2]恒成立…(2分).
當x=0時,cos0=cos0=1.
不妨取x=1,則cos1
2=cos1,所以cos1≠cos
21…(2分)
所以假設不成立,在集合M上,
函數f(x)與g(x)不是互為“H函數”…(1分).
(3)解:由題意得,a
x+1=a
x+1(a>0且a≠1)…(2分)
變形得,a
x(a-1)=1,
由于a>0且a≠1

,
因為a
x>0,所以

,即a>1…(2分)
此時x=-log
a(a-1),
集合M={x|x=-log
a(a-1),a>1}…(2分)
點評:本題考查函數值相等的證明,考查兩個函數是否互為“H函數”的判斷,考查滿足條件的實數的取值范圍的求法,解題時要認真審題,注意等價轉化思想的合理運用.

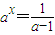 ,由此能求出a的取值范圍及集合M.
,由此能求出a的取值范圍及集合M. ,
, ,即a>1…(2分)
,即a>1…(2分)

 智慧課堂密卷100分單元過關檢測系列答案
智慧課堂密卷100分單元過關檢測系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案