
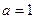 時, 求
時, 求 的單調區間、極值;
的單調區間、極值;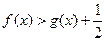 ;
;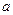 ,使
,使 的最小值是
的最小值是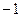 ,若存在,求出
,若存在,求出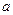 的值;若不存在,說明理由
的值;若不存在,說明理由 的的單調遞減區間為(0,1);單調遞增區間為(1,e);
的的單調遞減區間為(0,1);單調遞增區間為(1,e); 的極小值為
的極小值為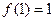
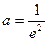
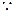 當
當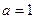 時,
時,
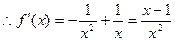 , 1分
, 1分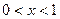 時,
時,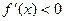 ,此時
,此時 單調遞減
單調遞減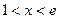 時,
時,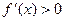 ,此時
,此時 單調遞增 …………………………………3分
單調遞增 …………………………………3分 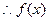 的的單調遞減區間為(0,1);單調遞增區間為(1,e);
的的單調遞減區間為(0,1);單調遞增區間為(1,e); 的極小值為
的極小值為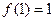 ………………………………………………4分
………………………………………………4分 在
在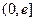 上的最小值為1, ……………………………………5分
上的最小值為1, ……………………………………5分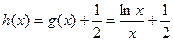 ,
,
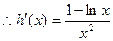 , ………………………6分
, ………………………6分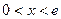 時,
時,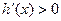 ,
,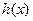 在
在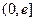 上單調遞增 …………………………………7分
上單調遞增 …………………………………7分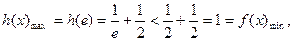 w
w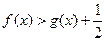 …………………………………………………8分
…………………………………………………8分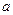 ,使
,使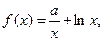 (
( )有最小值
)有最小值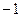 ,
,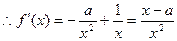 ……………………………………………………9分
……………………………………………………9分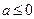 時,
時,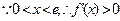 ,
,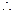
 在
在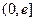 上單調遞增,此時
上單調遞增,此時 無最小值. …10分
無最小值. …10分 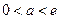 時,
時,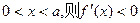 ,故
,故 在
在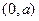 上單調遞減,
上單調遞減,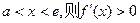 ,故
,故 在
在 上單調遞增.
上單調遞增.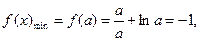 ,得
,得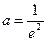 ,滿足條件. ……………………………12分
,滿足條件. ……………………………12分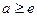 時,
時,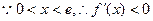 ,
,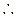
 在
在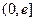 上單調遞減,
上單調遞減,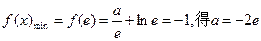 (舍去),
(舍去), 無最小值. ……13分
無最小值. ……13分 

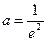 ,使得當
,使得當 時
時 的最小值是
的最小值是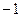 ……………………14分
……………………14分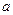 ,使
,使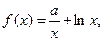
 的最小值是
的最小值是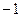 ,
,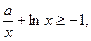 對
對 恒成立,求“等號”取得時實數a的值.
恒成立,求“等號”取得時實數a的值.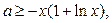 對
對 恒成立,求“等號”取得時實數a的值.
恒成立,求“等號”取得時實數a的值.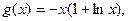 即
即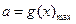 ,
, ………………10分
………………10分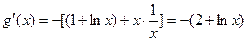 ……………………………11分
……………………………11分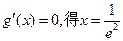
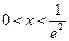 ,
,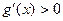 ,則
,則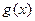 在
在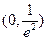 單調遞增;
單調遞增;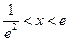 ,
,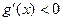 ,則
,則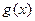 在
在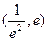 單調遞減. ……………………13分
單調遞減. ……………………13分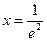 時,
時,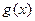 取得最大值,其值是
取得最大值,其值是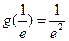 .
.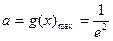
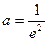 ,使得當
,使得當 時
時 的最小值是
的最小值是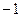 .……………………14分
.……………………14分

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com