【題目】等比數列{an}的各項均為正數，且2a1+3a2=1，a32=9a2a6 ， （Ⅰ）求數列{an}的通項公式；
（Ⅱ）設bn=log3a1+log3a2+…+log3an ， 求數列{ 
}的前n項和．
【答案】解：（Ⅰ）設數列{an}的公比為q，由a32=9a2a6得a32=9a42 ， 所以q2= 
． 由條件可知各項均為正數，故q= 
．
由2a1+3a2=1得2a1+3a1q=1，所以a1= ．
故數列{an}的通項式為an= 
．
（Ⅱ）bn= 
+ 
+…+ 
=﹣（1+2+…+n）=﹣ 
，
故 
=﹣ 
=﹣2（ 
﹣ 
）
則 
+ 
+…+ =﹣2[（1﹣ 
）+（ ﹣ ）+…+（ ﹣ ）]=﹣ 
，
所以數列{ }的前n項和為﹣
【解析】（Ⅰ）設出等比數列的公比q，由a32=9a2a6 ， 利用等比數列的通項公式化簡后得到關于q的方程，由已知等比數列的各項都為正數，得到滿足題意q的值，然后再根據等比數列的通項公式化簡2a1+3a2=1，把求出的q的值代入即可求出等比數列的首項，根據首項和求出的公比q寫出數列的通項公式即可；（Ⅱ）把（Ⅰ）求出數列{an}的通項公式代入設bn=log3a1+log3a2+…+log3an ， 利用對數的運算性質及等差數列的前n項和的公式化簡后，即可得到bn的通項公式，求出倒數即為 
的通項公式，然后根據數列的通項公式列舉出數列的各項，抵消后即可得到數列{ }的前n項和．
科目：高中數學 來源： 題型：
【題目】已知△ABC的三個內角分別為A，B，C，且A≠ 
．
（1）化簡 
；
（2）若角A滿足sinA+cosA= 
．
（i）試判斷△ABC是銳角三角形還是鈍角三角形，并說明理由；
（ii）求tanA的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=x3+bx2+cx的極值點為x=﹣ 
和x=1
（1）求b，c的值與f（x）的單調區間
（2）當x∈[﹣1，2]時，不等式f（x）＜m恒成立，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某超市連鎖店統計了城市甲、乙的各16臺自動售貨機在中午12：00至13：00間的銷售金額，并用莖葉圖表示如圖．則有（ ）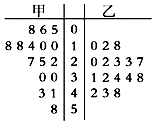 
A.甲城銷售額多，乙城不夠穩定
B.甲城銷售額多，乙城穩定
C.乙城銷售額多，甲城穩定
D.乙城銷售額多，甲城不夠穩定
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x），g（x）都是定義在R上的函數，且滿足以下條件：
①f（x）=axg（x）（a＞0，a≠1）；
②g（x）≠0；
③f（x）g'（x）＞f'（x）g（x）；
若 
，則a= ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）是定義在（﹣∞，+∞）上的增函數，實數a使得f（1﹣ax﹣x2）＜f（2﹣a）對于任意x∈[0，1]都成立，則實數a的取值范圍是（ ）
A.（﹣∞，1）
B.[﹣2，0]
C.（﹣2﹣2 
，﹣2+2 ）
D.[0，1]
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，點P在正方體ABCD﹣A1B1C1D1的面對角線BC1上運動，則下列四個結論：
①三棱錐A﹣D1PC的體積不變；
②A1P∥平面ACD1；
③DP⊥BC1；
④平面PDB1⊥平面ACD1 ．
其中正確的結論的個數是（ ）
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
