
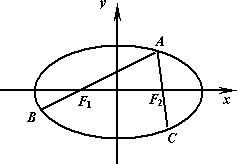
如圖,A為橢圓![]() 上的一個動點,弦AB、AC分別過焦點F1、F2,當AC垂直于x軸時,恰好有AF1∶AF2=3∶1.
上的一個動點,弦AB、AC分別過焦點F1、F2,當AC垂直于x軸時,恰好有AF1∶AF2=3∶1.
(Ⅰ)求橢圓的離心率;
(Ⅱ)設![]() .
.
①當A點恰為橢圓短軸的一個端點時,求λ1+λ2的值;
②當A點為該橢圓上的一個動點時,試判斷是λ1+λ2否為定值?若是,請證明;若不是,請說明理由.
解(Ⅰ)設![]() ,則
,則![]() .由題設及橢圓定義得
.由題設及橢圓定義得
![]() ,消去
,消去![]() 得
得![]() ,所以離心率
,所以離心率![]() .3分
.3分
(Ⅱ)解法一:由(1)知,![]() ,所以橢圓方程可化為
,所以橢圓方程可化為![]() .
.
①當A點恰為橢圓短軸的一個端點時,![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
由![]() 得
得 ![]() ,解得
,解得![]() ,
,
∴點![]() 的坐標為
的坐標為![]() .
.
又![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,
,![]() .6分
.6分
②當A點為該橢圓上的一個動點時,![]() 為定值6.
為定值6.
證明 設![]() ,
,![]() ,則
,則![]() .
.
若![]() 為橢圓的長軸端點,則
為橢圓的長軸端點,則![]() 或
或![]() ,
,
所以![]() .8分
.8分
若![]() 為橢圓上異于長軸端點的任意一點,則由
為橢圓上異于長軸端點的任意一點,則由![]() 得,
得,![]() ,所以
,所以![]() .
.
又直線![]() 的方程為
的方程為![]() ,所以由
,所以由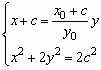 得
得
![]() .
.
![]() ,
,
∴![]() .
.
由韋達定理得 ![]() ,所以
,所以![]() .同理
.同理![]() .
.
∴![]() .
.
綜上證得,當A點為該橢圓上的一個動點時,![]() 為定值6.14分
為定值6.14分
解法二:設![]() ,
,![]() ,則
,則![]()
∵![]() ,∴
,∴![]() ;………………8分
;………………8分
又![]() ①,
①,![]() ②,將
②,將![]() 、
、![]() 代入②得:
代入②得:
![]() 即
即![]() ③;
③;
③![]() ①得:
①得:![]() ;……………12分
;……………12分
同理:由![]() 得
得![]() ,∴
,∴![]()
![]() ,∴
,∴![]() .…14分
.…14分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
 如圖,F1,F2是橢圓
如圖,F1,F2是橢圓| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 2 |
| 3 |
查看答案和解析>>
科目:高中數學 來源:2006-2007學年江蘇省無錫市濱湖區高二(上)期中數學試卷(解析版) 題型:解答題
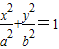 (a>b>0)上的焦點,P為橢圓上的點,PF1⊥OX軸,且OP和橢圓的一條長軸頂點A和短軸頂點B的連線AB平行.
(a>b>0)上的焦點,P為橢圓上的點,PF1⊥OX軸,且OP和橢圓的一條長軸頂點A和短軸頂點B的連線AB平行.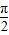
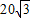 ,求橢圓方程.
,求橢圓方程.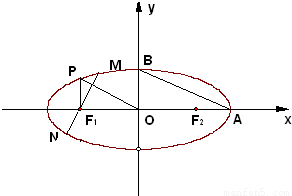
查看答案和解析>>
科目:高中數學 來源:2012年湖北省黃岡中學高三適應性考試數學試卷(理科)(解析版) 題型:選擇題
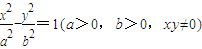 上的動點,F1、F2是雙曲線的焦點,M是∠F1PF2的平分線上的一點,且
上的動點,F1、F2是雙曲線的焦點,M是∠F1PF2的平分線上的一點,且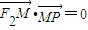 .有一同學用以下方法研究|OM|:延長F2M交PF1于點N,可知△PNF2為等腰三角形,且M為F2N的中點,得
.有一同學用以下方法研究|OM|:延長F2M交PF1于點N,可知△PNF2為等腰三角形,且M為F2N的中點,得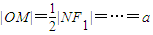 .類似地:P是橢圓
.類似地:P是橢圓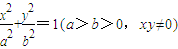 上的動點,F1、F2是橢圓的焦點,M是∠F1PF2的平分線上的一點,且
上的動點,F1、F2是橢圓的焦點,M是∠F1PF2的平分線上的一點,且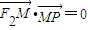 .則|OM|的取值范圍是( )
.則|OM|的取值范圍是( )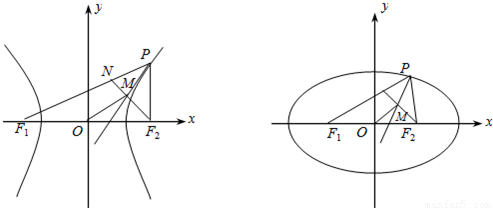
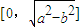
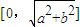
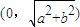
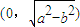
查看答案和解析>>
科目:高中數學 來源:2010-2011學年江西省重點中學協作體高三第三次聯考數學試卷(理科)(解析版) 題型:解答題
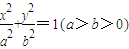 上的一個動點,F1,F2分別為橢圓的左、右焦點,弦AB過點F2,當AB⊥x軸時,恰好有|AF1|=3|AF2|.
上的一個動點,F1,F2分別為橢圓的左、右焦點,弦AB過點F2,當AB⊥x軸時,恰好有|AF1|=3|AF2|.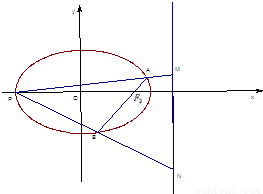
查看答案和解析>>
科目:高中數學 來源:2011年江西省高考數學仿真押題卷10(理科)(解析版) 題型:解答題
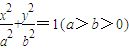 上的一個動點,F1,F2分別為橢圓的左、右焦點,弦AB過點F2,當AB⊥x軸時,恰好有|AF1|=3|AF2|.
上的一個動點,F1,F2分別為橢圓的左、右焦點,弦AB過點F2,當AB⊥x軸時,恰好有|AF1|=3|AF2|.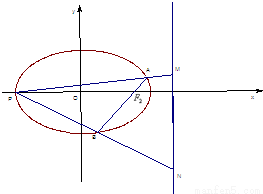
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com